
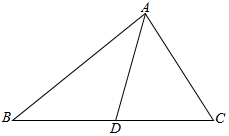
 如图,在△ABC中,∠C=60°,D是BC上一点,AB=31,BD=20,AD=21.
如图,在△ABC中,∠C=60°,D是BC上一点,AB=31,BD=20,AD=21.分析 (1)利用余弦定理可得cosB=$\frac{A{B}^{2}+B{D}^{2}-A{D}^{2}}{2AB•BD}$.
(2)0°<B<180°,由(1)可得:sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{12\sqrt{3}}{31}$,可得sin∠BAC=sin[180°-(B+60°)]=sin(B+60°).
在△ABC中,由正弦定理可得:$\frac{BC}{sin∠BAC}$=$\frac{AB}{sin∠C}$,即可得出.
解答 解:(1)在△ABC中,cosB=$\frac{A{B}^{2}+B{D}^{2}-A{D}^{2}}{2AB•BD}$=$\frac{3{1}^{2}+2{0}^{2}-2{1}^{2}}{2×31×20}$=$\frac{23}{31}$.
(2)0°<B<180°,由(1)可得:sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{12\sqrt{3}}{31}$,
∴sin∠BAC=sin[180°-(B+60°)]=sin(B+60°)=sinBcos60°+cosBsin60°=$\frac{1}{2}×\frac{12\sqrt{3}}{31}$+$\frac{23}{31}×\frac{\sqrt{3}}{2}$=$\frac{35\sqrt{3}}{62}$.
在△ABC中,由正弦定理可得:$\frac{BC}{sin∠BAC}$=$\frac{AB}{sin∠C}$,
∴BC=$\frac{ABsin∠BAC}{sin∠C}$=$\frac{31×\frac{35\sqrt{3}}{62}}{\frac{\sqrt{3}}{2}}$=35.
点评 本题考查了正弦定理余弦定理、和差公式、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 若p,q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件 | |
| B. | 若p为:?x∈R,x2+2x≤0则¬p为:?x∈R,x2+2x>0 | |
| C. | 命题p为真命题,命题q为假命题.则命题p∧(¬q),(¬p)∨q都是真命题 | |
| D. | 命题“若¬p,则q”的逆否命题是“若p,则¬q”. |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | -$\sqrt{2}$ | C. | ±$\sqrt{3}$ | D. | ±$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 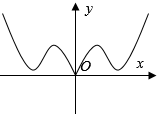 | ||
| C. |  | D. | 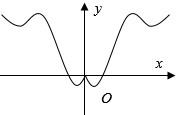 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com