
| A、命题“?x∈R,使得x2+x-1>0”的否定是“?x∈R,x2+x-1<0” | ||
B、命题p:“?x∈R,sinx+cosx≤
| ||
| C、“x=-1”是“x2-2x-3=0”的必要不充分条件 | ||
| D、“0<a<1”是“函数f(x)=ax(a>0,a≠1)在R上为减函数”的充要条件 |
| 2 |
| π |
| 4 |
| 2 |


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
| 1-ex |
| 1+ex |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、[-1,+∞) |
| B、[1,+∞) |
| C、(-∞,1] |
| D、(-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某校高三年级从一次模拟考试中随机抽取50名学生(男、女生各25名),将数学成绩进行统计,所得数据的茎叶图如图所示,以组距为10将数据按[80,90),[90,100),…,[130,140),[140,150]分成七组绘制频率分布直方图,则落在区间[130,140)的小矩形的面积为( )
某校高三年级从一次模拟考试中随机抽取50名学生(男、女生各25名),将数学成绩进行统计,所得数据的茎叶图如图所示,以组距为10将数据按[80,90),[90,100),…,[130,140),[140,150]分成七组绘制频率分布直方图,则落在区间[130,140)的小矩形的面积为( )| A、1.2 | B、6 |
| C、0012 | D、0.12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(1,2) | ||
| B、(2,3) | ||
C、(
| ||
D、(0,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
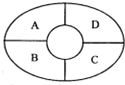 如图某综艺节目现场设有A、B、C、D四个观众席,现有由3中不同颜色与2种不同款式组成的6中马甲安排给现场观众,要求每个观众席上的马甲相同,相邻观众席上的马甲的颜色与款式都不相同,则不同的安排方法种数为( )
如图某综艺节目现场设有A、B、C、D四个观众席,现有由3中不同颜色与2种不同款式组成的6中马甲安排给现场观众,要求每个观众席上的马甲相同,相邻观众席上的马甲的颜色与款式都不相同,则不同的安排方法种数为( )| A、72 | B、96 | C、36 | D、48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com