
分析 设等比数列{an}的公比为q>0,an>0,a1=256,S3=448,可得256(1+q+q2)=448,解得q.Tn为数列{an}的前n项乘积,则T17=${a}_{1}^{17}$q0+1+2+…+16=$({a}_{1}{q}^{8})^{17}$.即可得出.
解答 解:设等比数列{an}的公比为q>0,an>0,a1=256,S3=448,
∴256(1+q+q2)=448,
解得q=$\frac{1}{2}$.
Tn为数列{an}的前n项乘积,则T17=${a}_{1}^{17}$q0+1+2+…+16=$25{6}^{17}×{q}^{\frac{16(1+16)}{2}}$=$({a}_{1}{q}^{8})^{17}$=$(256×\frac{1}{{2}^{8}})^{17}$=1.
故答案为:1.
点评 本题考查了等比数列的通项公式及其前n项和的性质、指数的运算性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
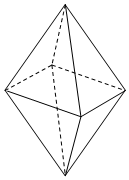 已知四面体的6条棱所在的直线中有3对异面直线,那么在过正八面体(由2个棱长相同的四棱锥拼接而成,如图所示)的任意2个顶点的所有直线中,随机取2条,则这2条直线异面的情况有24种.
已知四面体的6条棱所在的直线中有3对异面直线,那么在过正八面体(由2个棱长相同的四棱锥拼接而成,如图所示)的任意2个顶点的所有直线中,随机取2条,则这2条直线异面的情况有24种.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln(x+y)=lnx+lny | B. | $\frac{lgx}{lgy}$=lg$\frac{x}{y}$ | C. | lg$\frac{x}{y}$=lgx-lgy | D. | lg(xy)=lgx•lgy |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-tanx | B. | $y=cos(2x-\frac{π}{2})$ | C. | y=sin2x+cos2x | D. | y=2cos2x-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①③④ | C. | ②③④ | D. | ①④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com