
分析 (1)利用双曲线的定义及其标准方程即可得出;
(2)当直线l的斜率存在时,设直线方程为y=k(x-2),P(x1,y1),Q(x2,y2),与双曲线方程联立消y得(k2-3)x2-4k2x+4k2+3=0,利用根与系数的关系、判别式解出即可得出.
(i)利用向量垂直与数量积的关系、根与系数的关系即可得出;
(ii)利用点到直线的距离公式、弦长公式、点到直线的距离公式、三角形的面积计算公式即可得出.
解答 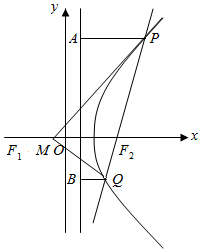 解:(1)由|PF1|-|PF2|=2<|F1F2|知,点P的轨迹E是以F1、F2为焦点的双曲线右支,
解:(1)由|PF1|-|PF2|=2<|F1F2|知,点P的轨迹E是以F1、F2为焦点的双曲线右支,
由c=2,2a=2,∴b2=3,
故轨迹E的方程为${x^2}-\frac{y^2}{3}=1(x≥1)$.--(3分)
(2)当直线l的斜率存在时,设直线方程为y=k(x-2),P(x1,y1),Q(x2,y2),
与双曲线方程联立消y得(k2-3)x2-4k2x+4k2+3=0,∴$\left\{\begin{array}{l}{k^2}-3≠0\\△>0\\{x_1}+{x_2}=\frac{{4{k^2}}}{{{k^2}-3}}>0\\{x_1}•{x_2}=\frac{{4{k^2}+3}}{{{k^2}-3}}>0\end{array}\right.$,解得k2>3--(5分)
(i)∵$\overrightarrow{MP}•\overrightarrow{MQ}=({x_1}-m)({x_2}-m)+{y_1}{y_2}$
$\begin{array}{l}=({x_1}-m)({x_2}-m)+{k^2}({x_1}-2)({x_2}-2)\\=({k^2}+1){x_1}{x_2}-(2{k^2}+m)({x_1}+{x_2})+{m^2}+4{k^2}\\=\frac{{({k^2}+1)(4{k^2}+3)}}{{{k^2}-3}}-\frac{{4{k^2}(2{k^2}+m)}}{{{k^2}-3}}+{m^2}+4{k^2}\\=\frac{{3-(4m+5){k^2}}}{{{k^2}-3}}+{m^2}.…(7分)\end{array}$∵MP⊥MQ,∴$\overrightarrow{MP}•\overrightarrow{MQ}=0$,
故得3(1-m2)+k2(m2-4m-5)=0对任意的k2>3恒成立,
∴$\left\{\begin{array}{l}1-{m^2}=0\\{m^2}-4m-5=0\end{array}\right.,解得m=-1$.∴当m=-1时,MP⊥MQ.
当直线l的斜率不存在时,由P(2,3),Q(2,-3)及M(-1,0)知结论也成立,
综上,当m=-1时,MP⊥MQ.--(8分)
(ii)由(i)知,M(-1,0),当直线l的斜率存在时,$|{PQ}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=6\frac{{1+{k^2}}}{{{k^2}-3}}$,M点到直线PQ的距离为d,则$d=\frac{3|k|}{{\sqrt{1+{k^2}}}}$
∴${S_{△MPQ}}=\frac{1}{2}|{PQ}|d=9\frac{{|k|\sqrt{1+{k^2}}}}{{{k^2}-3}}=9\frac{{\sqrt{(1+{k^2}){k^2}}}}{{{k^2}-3}}=9\sqrt{\frac{{(1+{k^2}){k^2}}}{{{{({k^2}-3)}^2}}}}$--(10分)
令k2-3=t(t>0),则${S_{△MPQ}}=9\sqrt{\frac{12}{t^2}+\frac{7}{t}+1}$,因为$\frac{1}{t}>0$
所以${S_{△MPQ}}=9\sqrt{\frac{12}{t^2}+\frac{7}{t}+1}>9$--(12分)
当直线l的斜率不存在时,${S_{△MPQ}}=\frac{1}{2}•3•6=9$--(13分)
综上可知S△MPQ≥9,故S△MPQ的最小值为9.--(14分)
点评 本题考查了双曲线的标准方程及其性质、直线与双曲线相交问题、向量垂直与数量积的关系、一元二次方程的根与系数的关系、点到直线的距离公式、弦长公式、点到直线的距离公式、三角形的面积计算公式、向量垂直与数量积的关系,考查了推理能力与计算能力,属于难题.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,0) | B. | $(-\frac{π}{3},0)$ | C. | $(\frac{π}{3},0)$ | D. | $(\frac{π}{6},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 63、64、66 | B. | 65、65、67 | C. | 65、64、66 | D. | 64、65、64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②⑥ | C. | ③⑤ | D. | ④⑥ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [kπ+$\frac{π}{8}$,kπ+$\frac{5}{8}$π] | B. | [kπ-$\frac{3}{8}$π,kπ+$\frac{π}{8}$] | C. | [2kπ+$\frac{π}{8}$,2kπ+$\frac{5}{8}$π] | D. | [2kπ-$\frac{3}{8}$π,2kπ+$\frac{π}{8}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com