练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．下列各式正确的题目序号有（　　）
    ①log26-log23=log23     
    ②log39=3       
    ③$\root{4}{{{{（-3）}^4}}}=-3$
    ④20.1＜20.2
    ⑤log0.72.1＞log0.71.9       
    ⑥${0.9^{\frac{1}{2}}}＞{0.8^{\frac{1}{2}}}$．
    A．①④B．②⑥C．③⑤D．④⑥

    分析 分别根据基本函数的运算性质和函数的单调性判断即可．

    解答 解：①log26-log23=log22=1，
    ②log39=2，
    ③$\root{4}{（-3）^{4}}$=3，
    ④20.1＜20.2
    ⑤log0.72.1＜log0.71.9       
    ⑥${0.9^{\frac{1}{2}}}＞{0.8^{\frac{1}{2}}}$．
    故正确的有④⑥，
    故选：D．

    点评 本题考查了基本函数的运算性质，以及基本函数的单调性，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．下列函数是正态分布密度函数的是（　　）
    A．f（x）=$\frac{1}{{\sqrt{2π}σ}}{e^{\frac{{{{（x-r）}^2}}}{2σ}}}$B．f（x）=$\frac{{\sqrt{2π}}}{2π}{e^{-\frac{x^2}{2}}}$
    C．f（x）=$\frac{1}{{2\sqrt{2}π}}{e^{\frac{{{{（x-1）}^2}}}{4}}}$D．f（x）=$\frac{1}{{\sqrt{2π}}}{e^{\frac{x^2}{2}}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．由2个人在一座8层大楼的底层进入电梯，假设每一个人自第二层开始在每一层离开电梯是等可能的，则这两个人在不同层离开电梯的概率是（　　）
    A．$\frac{7}{8}$B．$\frac{6}{7}$C．$\frac{5}{6}$D．$\frac{36}{49}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知△ABC的顶点B、C在椭圆$\frac{x^2}{12}+\frac{y^2}{3}=1$上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是（　　）
    A．$8\sqrt{3}$B．6C．$4\sqrt{3}$D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

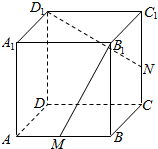    4．如图所示，在正方体ABCD-A1B1C1D1中，M，N分别是线段AB，CC1的中点，∨MB1P的顶点P在棱CC1与棱C1D1上运动，有以下四个命题：
    ①平面MB1P⊥ND1
    ②平面MB1P⊥平面ND1A1
    ③∨MB1P在底面ABCD上的射影图形的面积为定值；
    ④△MB1P在侧面DD1C1C上的射影图形是三角形．
    其中正确的命题序号是（　　）
    A．①B．①③C．②③D．②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．下列函数中，既是偶函数又在（0，+∞）上单调递增的是（　　）
    A．y=x3B．y=|x|+1C．y=-x2+1D．y=（$\frac{1}{2}$）X

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知F1（-2，0），F2（2，0），点P满足|PF1|-|PF2|=2，记点P的轨迹为E．
    （1）求轨迹E的方程；
    （2）若直线l过点F2且与轨迹E交于P、Q两点．
    （i）无论直线l绕点F2怎样转动，在x轴上总存在定点M（m，0），使MP⊥MQ恒成立，求实数m的值．
    （ii）在（i）的条件下，求△MPQ面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知$\overrightarrow{a}$，$\overrightarrow{b}$是单位向量，且$\overrightarrow{a}•\overrightarrow{b}$=-$\frac{1}{2}$．若平面向量$\overrightarrow{p}$满足$\overrightarrow{p}•\overrightarrow{a}$=$\overrightarrow{p}•\overrightarrow{b}$=$\frac{1}{2}$，则|$\overrightarrow{p}$|=（　　）
    A．2B．$\sqrt{2}$C．1D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．△ABC的内角A，B，C的对边分别为a，b，c，已知$\frac{sinA-sinB}{sinC}$=$\frac{b+c}{a+b}$，
    （1）求角A的大小；
    （2）求4sinB•cosC的取值范围．

    查看答案和解析>>

    同步练习册答案