
| A. | f(x)=$\frac{1}{{\sqrt{2π}σ}}{e^{\frac{{{{(x-r)}^2}}}{2σ}}}$ | B. | f(x)=$\frac{{\sqrt{2π}}}{2π}{e^{-\frac{x^2}{2}}}$ | ||
| C. | f(x)=$\frac{1}{{2\sqrt{2}π}}{e^{\frac{{{{(x-1)}^2}}}{4}}}$ | D. | f(x)=$\frac{1}{{\sqrt{2π}}}{e^{\frac{x^2}{2}}}$ |
分析 直接在正态密度函数f(x)=$\frac{1}{\sqrt{2π}δ}{e}^{-\frac{(x-μ)^{2}}{2{δ}^{2}}}$中去μ=0,δ=1得答案.
解答 解:由正态密度函数的特征f(x)=$\frac{1}{\sqrt{2π}δ}{e}^{-\frac{(x-μ)^{2}}{2{δ}^{2}}}$可知,
当δ=1,μ=0时,正态密度函数f(x)=$\frac{1}{\sqrt{2π}δ}{e}^{-\frac{(x-μ)^{2}}{2{δ}^{2}}}$=$\frac{{\sqrt{2π}}}{2π}{e^{-\frac{x^2}{2}}}$=$\frac{1}{\sqrt{2π}}{e}^{-\frac{{x}^{2}}{2}}$为标准正态密度函数,
故选:B.
点评 本题考查正态分布曲线的特点及曲线所表示的意义,关键是熟记正态密度函数的特征,是基础题.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
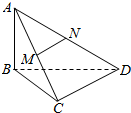 如图所示,已知AB⊥平面BCD,M,N分别是AC,AD的中点,BC⊥CD.
如图所示,已知AB⊥平面BCD,M,N分别是AC,AD的中点,BC⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,0) | B. | $(-\frac{π}{3},0)$ | C. | $(\frac{π}{3},0)$ | D. | $(\frac{π}{6},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②⑥ | C. | ③⑤ | D. | ④⑥ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com