
分析 设AB:y=kx+2,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根与系数的关系利用切线的几何意义即可求得过抛物线上A、B两点的切线斜率关系,从而解决问题
解答 证明:∵直线AB与x轴不垂直,设AB:y=kx+2,A(x1,y1),B(x2,y2).
由$\left\{\begin{array}{l}{y=kx+2}\\{y=\frac{1}{8}{x}^{2}}\end{array}\right.$得到x2-8kx-16=0,x1+x2=8k,x1x2=-16,
抛物线方程为y=$\frac{1}{8}$x2,
∴y′=$\frac{1}{4}$x
∴过抛物线上A、B两点的切线斜率分别是k1=$\frac{1}{4}$x1,k2=$\frac{1}{4}$x2,
∴k1•k2=$\frac{1}{4}$x1•$\frac{1}{4}$x2=-1,
∴AQ⊥BQ
点评 本题考查抛物线的定义和性质得应用和导数的几何意义,考查运算求解能力,考查数形结合思想,解答的关键利用是抛物线定义,体现了转化的数学思想..


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 已知ABCD是矩形,设PA=a,PA⊥平面ABCD,M、N分别是AB、PC的中点.
已知ABCD是矩形,设PA=a,PA⊥平面ABCD,M、N分别是AB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
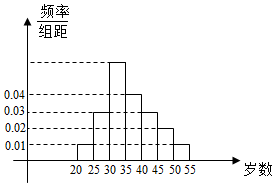 某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人.
某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
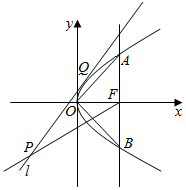 已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合).
已知抛物线C:y2=2px(p>0)的焦点为F,过F作垂直于x轴的直线交抛物线于A,B,两点,△AOB的面积为8,直线l与抛物线C相切于Q点,P是l上一点(不与Q重合).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com