
已知各项均不为零的数列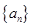 ,其前n项和
,其前n项和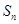 满足
满足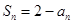 ;等差数列
;等差数列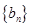 中
中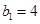 ,且
,且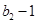 是
是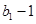 与
与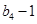 的等比中项
的等比中项
(1)求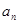 和
和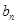 ,
,
(2)记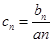 ,求
,求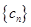 的前n项和
的前n项和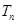 .
.
(1)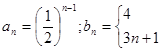
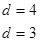 ;(2)
;(2)
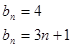 .
.
解析试题分析:(1)通过 求
求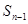 ,然后两式相减得出
,然后两式相减得出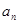 的递推形式,
的递推形式,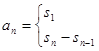
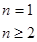 ,不要忘了验证
,不要忘了验证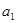 是否满足
是否满足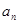 ,从而求出
,从而求出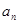 的通项公式,
的通项公式, 为等差数列,设
为等差数列,设 ,按照这三项成等比数列,可以通过已知建立方程求出
,按照这三项成等比数列,可以通过已知建立方程求出 ,然后求出
,然后求出 通项;(2)分类讨论思想,(1)问求出,
通项;(2)分类讨论思想,(1)问求出, 的通项公式有两个,所以
的通项公式有两个,所以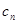 也是两个,其中
也是两个,其中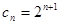 或
或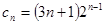 ,第一个通项公式按等比数列的前N项和求解,第二个按错位相减法,列出
,第一个通项公式按等比数列的前N项和求解,第二个按错位相减法,列出 ,再列出q
,再列出q ,
,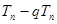 ,求出
,求出 .运算量比较大.平时要加强训练.此题为中档题.
.运算量比较大.平时要加强训练.此题为中档题.
试题解析:(1)对于数列 由题可知
由题可知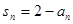 ①
①
当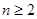 时,
时, ②
②
①-②得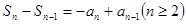 1分
1分
即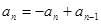 ,
,
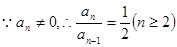 2分
2分
又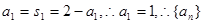 是以1为首项,以
是以1为首项,以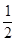 为公比的等比数列
为公比的等比数列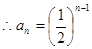 3分
3分
设等差数列 的公比为
的公比为 ,由题知
,由题知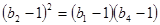 4分
4分
又
 ,解得
,解得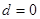 或
或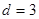
当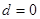 时,
时,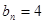 ;当
;当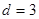 时,
时,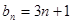 6分
6分
(2)当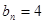 时,
时,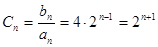
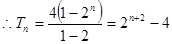 7分
7分
当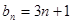 时,
时,
此时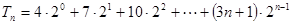 ③
③ ④ 8分
④ 8分
③-④得
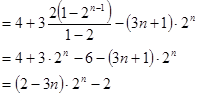
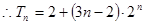 11分
11分
综上: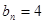 时,
时,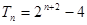 ;
;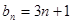 时,
时,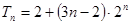 12分
12分
考点:1.等差,等比数列的通项公式,性质;2.已知 求
求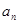 ;3.错位相减法求和.
;3.错位相减法求和.


科目:高中数学 来源: 题型:解答题
某校高一学生1000人,每周一次同时在两个可容纳600人的会议室,开设“音乐欣赏”与“美术鉴赏”的校本课程.要求每个学生都参加,要求第一次听“音乐欣赏”课的人数为
 ,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用
,其余的人听“美术鉴赏”课;从第二次起,学生可从两个课中自由选择.据往届经验,凡是这一次选择“音乐欣赏”的学生,下一次会有20﹪改选“美术鉴赏”,而选“美术鉴赏”的学生,下次会有30﹪改选“音乐欣赏”,用 分别表示在第
分别表示在第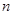 次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
次选“音乐欣赏”课的人数和选“美术鉴赏”课的人数.
(1)若 ,分别求出第二次,第三次选“音乐欣赏”课的人数
,分别求出第二次,第三次选“音乐欣赏”课的人数 ;
;
(2)①证明数列 是等比数列,并用
是等比数列,并用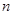 表示
表示 ;
;
②若要求前十次参加“音乐欣赏”课的学生的总人次不超过5800,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设数列{bn}满足bn+2=-bn+1-bn(n∈N*),b2=2b1.
(1)若b3=3,求b1的值;
(2)求证数列{bnbn+1bn+2+n}是等差数列;
(3)设数列{Tn}满足:Tn+1=Tnbn+1(n∈N*),且T1=b1=- ,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知公差不为0的等差数列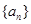 的前3项和
的前3项和 =9,且
=9,且 成等比数列
成等比数列
(1)求数列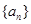 的通项公式和前n项和
的通项公式和前n项和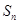 ;
;
(2)设 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值
的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
称满足以下两个条件的有穷数列 为
为 阶“期待数列”:
阶“期待数列”:
① ;②
;② .
.
(1)若等比数列 为
为 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及 的通项公式;
的通项公式;
(2)若一个等差数列 既是
既是 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记n阶“期待数列”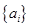 的前k项和为
的前k项和为 :
:
(i)求证: ;
;
(ii)若存在 使
使 ,试问数列
,试问数列 能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com