
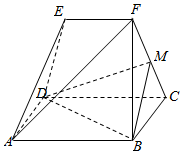
 如图,已知在多面体ABCDEF中,ABCD为正方形,EF∥平面ABCD,M为FC的中点,AB=2,EF到平面ABCD的距离为2,FC=2.
如图,已知在多面体ABCDEF中,ABCD为正方形,EF∥平面ABCD,M为FC的中点,AB=2,EF到平面ABCD的距离为2,FC=2.分析 (1)根据线面平行的判定定理,即可证明AF∥平面MBD;
(2)若EF=1,证明EF⊥平面FBC即EF是三棱锥的高,结合三棱锥的体积公式即可求VF-MBE.
解答 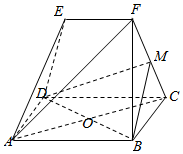 解:(1)证明:连接AC,设AC与BD交于O点,在正方形ABCD中,O为AC的中点.
解:(1)证明:连接AC,设AC与BD交于O点,在正方形ABCD中,O为AC的中点.
∵M是FC的中点,
∴OM∥AF,
∵AF?平面MBD,OM?平面MBD,
∴AF∥平面MBD.
(2)∵EF∥平面ABCD,FC=2,EF到平面ABCD的距离为2,
∴FC⊥平面ABCD,平面FBC⊥平面ABCD,
∵四边形ABCD为正方形,则AB⊥平面FBC,
∵EF∥平面ABCD,
∴EF∥AB,∴EF⊥平面FBC.
${V_{F-MNE}}={V_{E-FNM}}=\frac{1}{3}EF•{S_{△FNM}}=\frac{1}{3}×1×\frac{1}{2}×2×2=\frac{2}{3}$.
点评 本题主要考查线面平行的判定以及三棱锥体积的计算,根据相应的判定定理以及三棱锥的体积公式是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 0.6 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高血压 | 非高血压 | 总计 | |
| 年龄20到39岁 | 12 | c | 100 |
| 年龄40到60岁 | b | 52 | 100 |
| 总计 | 60 | a | 200 |
| P(k2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{7}{8}$ | B. | $\frac{7}{8}$ | C. | $\frac{7}{8}$或$-\frac{7}{8}$ | D. | $\frac{{\sqrt{15}}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com