
【题目】如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1
(Ⅰ)设为P为AC的中点,Q为AB上一点,使PQ⊥OA,并计算 ![]() 的值;
的值;
(Ⅱ)求二面角O﹣AC﹣B的平面角的余弦值.
【答案】解:法一:
(Ⅰ)在平面OAB内作ON⊥OA交AB于N,连接NC.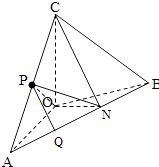
又OA⊥OC,∴OA⊥平面ONC
∵NC平面ONC,
∴OA⊥NC.
取Q为AN的中点,则PQ∥NC.
∴PQ⊥OA
在等腰△AOB中,∠AOB=120°,
∴∠OAB=∠OBA=30°
在Rt△AON中,∠OAN=30°,
∴ ![]()
在△ONB中,∠NOB=120°﹣90°=30°=∠NBO,
∴NB=ON=AQ.
∴ ![]()
(Ⅱ)连接PN,PO,
由OC⊥OA,OC⊥OB知:OC⊥平面OAB.
又ON平面OAB,
∴OC⊥ON
又由ON⊥OA,ON⊥平面AOC.
∴OP是NP在平面AOC内的射影.
在等腰Rt△COA中,P为AC的中点,
∴AC⊥OP
根据三垂线定理,知:
∴AC⊥NP
∴∠OPN为二面角O﹣AC﹣B的平面角
在等腰Rt△COA中,OC=OA=1,∴ ![]()
在Rt△AON中, ![]() ,
,
∴在Rt△PON中, ![]() .
.
∴ 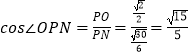
解法二:
(I)取O为坐标原点,分别以OA,OC所在的直线为x轴,z轴,
建立空间直角坐标系O﹣xyz(如图所示)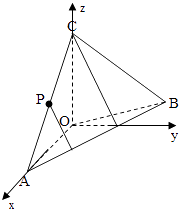
则 ![]()
∵P为AC中点,∴ ![]()
设 ![]() ,∵
,∵ ![]() .
.
∴ ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() 即
即 ![]() ,
, ![]() .
.
所以存在点 ![]() 使得PQ⊥OA且
使得PQ⊥OA且 ![]() .
.
(Ⅱ)记平面ABC的法向量为 ![]() =(n1 , n2 , n3),则由
=(n1 , n2 , n3),则由 ![]() ,
, ![]() ,
,
得 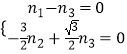 ,故可取
,故可取 ![]()
又平面OAC的法向量为 ![]() =(0,1,0).
=(0,1,0).
∴cos< ![]() ,
, ![]() >=
>= ![]() .
.
两面角O﹣AC﹣B的平面角是锐角,记为θ,则 ![]()
【解析】解法一:(1)要计算 ![]() 的值,我们可在平面OAB内作ON⊥OA交AB于N,连接NC.则根据已知条件结合平面几何中三角形的性质我们易得NB=ON=AQ,则易求出
的值,我们可在平面OAB内作ON⊥OA交AB于N,连接NC.则根据已知条件结合平面几何中三角形的性质我们易得NB=ON=AQ,则易求出 ![]() 的值.(2)要求二面角O﹣AC﹣B的平面角的余弦值,我们可连接PN,PO,根据三垂线定理,易得∠OPN为二面角O﹣AC﹣B的平面角,然后解三角形OPN得到二面角O﹣AC﹣B的平面角的余弦值.
的值.(2)要求二面角O﹣AC﹣B的平面角的余弦值,我们可连接PN,PO,根据三垂线定理,易得∠OPN为二面角O﹣AC﹣B的平面角,然后解三角形OPN得到二面角O﹣AC﹣B的平面角的余弦值.
解法二:取O为坐标原点,分别以OA,OC所在的直线为x轴,z轴,建立空间直角坐标系O﹣xyz,我们易根据已知给出四面体中各点的坐标,利用向量法进行求解,(1)由A、Q、B三点共线,我们可设 ![]() ,然后根据已知条件,构造关于λ的方程,解方程即可得到λ的值,即
,然后根据已知条件,构造关于λ的方程,解方程即可得到λ的值,即 ![]() 的值;(2)要求二面角O﹣AC﹣B的平面角的余弦值,我们可以分别求出平面OAC及平面ABC的法向量,然后根据求二面角O﹣AC﹣B的平面角的余弦值等于两个法向量夹角余弦的绝对值进行求解.
的值;(2)要求二面角O﹣AC﹣B的平面角的余弦值,我们可以分别求出平面OAC及平面ABC的法向量,然后根据求二面角O﹣AC﹣B的平面角的余弦值等于两个法向量夹角余弦的绝对值进行求解.
【考点精析】根据题目的已知条件,利用平面与平面之间的位置关系的相关知识可以得到问题的答案,需要掌握两个平面平行没有交点;两个平面相交有一条公共直线.


科目:高中数学 来源: 题型:
【题目】为了调查高中学生喜欢打羽毛球与性别是否有关,调查人员就“是否喜欢打羽毛球”这个问题,分别随机调查了![]() 名女生和
名女生和![]() 名男生,根据调查结果得到如图所示的等高条形图:
名男生,根据调查结果得到如图所示的等高条形图:

(1)完成下列![]() 列联表:
列联表:
喜欢打羽毛球 | 不喜欢打羽毛球 | 总计 | |
女生 | |||
男生 | |||
总计 |
(2)能否在犯错误的概率不超过![]() 的前提下认为喜欢打羽毛球与性别有关.
的前提下认为喜欢打羽毛球与性别有关.
参考数表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,可见部分如下:

试根据图表中的信息解答下列问题:
(1)求全班的学生人数及分数在[70,80)之间的频数;
(2)为快速了解学生的答题情况,老师按分层抽样的方法从位于[70,80),[80,90)和[90,100]分数段的试卷中抽取8份进行分析,再从中任选3人进行交流,求交流的学生中,成绩位于[70,80)分数段的人数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 f(x)=loga(x+1)﹣loga(1﹣x),a>0 且 a≠1.
(1)判断 f(x)的奇偶性并予以证明;
(2)当 a>1 时,求使 f(x)>0 的 x 的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知线段![]() 上有
上有![]() 个确定的点(包括端点
个确定的点(包括端点![]() 与
与![]() ).现对这些点进行往返标数(从
).现对这些点进行往返标数(从![]() …进行标数,遇到同方向点不够数时就“调头”往回数).如图:在点
…进行标数,遇到同方向点不够数时就“调头”往回数).如图:在点![]() 上标
上标![]() ,称为点
,称为点![]() ,然后从点
,然后从点![]() 开始数到第二个数,标上
开始数到第二个数,标上![]() ,称为点
,称为点![]() ,再从点
,再从点![]() 开始数到第三个数,标上
开始数到第三个数,标上![]() ,称为点
,称为点![]() (标上数
(标上数![]() 的点称为点
的点称为点![]() ),……,这样一直继续下去,直到
),……,这样一直继续下去,直到![]() ,
,![]() ,
,![]() ,…,
,…,![]() 都被标记到点上,则点
都被标记到点上,则点![]() 上的所有标记的数中,最小的是_______.
上的所有标记的数中,最小的是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,四边形ADEF为梯形,AD//FE,∠AFE=60,且平面ABCD⊥平面ADEF,AF=FE=AB=![]() =2,点G为AC的中点.
=2,点G为AC的中点.

(1)求证:EG//平面ABF;
(2)求三棱锥B-AEG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 均为非负整数,在做
均为非负整数,在做![]() 的加法时各位均不进位(例如,
的加法时各位均不进位(例如,![]() ),则称
),则称![]() 为“简单的”有序对,而
为“简单的”有序对,而![]() 称为有序数对
称为有序数对![]() 的值,那么值为2964的“简单的”有序对的个数是( )
的值,那么值为2964的“简单的”有序对的个数是( )
A. 525 B. 1050 C. 432 D. 864
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线C:x2=4y,点P是C的准线l上的动点,过点P作C的两条切线,切点分别为A,B,则△AOB面积的最小值为( )
A.![]()
B.2
C.2 ![]()
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,且直线
,且直线![]() 是其图象的一条对称轴.
是其图象的一条对称轴.
(1)求函数![]() 的解析式;
的解析式;
(2)在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边分别为
所对的边分别为![]() 、
、![]() 、
、![]() ,且
,且![]() ,
,![]() ,若
,若![]() 角满足
角满足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的
个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的![]() 倍后所得到的图象对应的函数记作
倍后所得到的图象对应的函数记作![]() ,已知常数
,已知常数![]() ,
,![]() ,且函数
,且函数![]() 在
在![]() 内恰有
内恰有![]() 个零点,求常数
个零点,求常数![]() 与
与![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com