练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，已知是圆的直径，，在圆上且分别在的两侧，其中，.现将其沿折起使得二面角为直二面角，则下列说法不正确的是（ ）

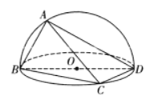
    A.，，，在同一个球面上

    B.当时，三棱锥的体积为

    C.与是异面直线且不垂直

    D.存在一个位置，使得平面平面

    【答案】D

    【解析】

    依次判断每个选项的正误：，所以A正确；当，A，C各在所在圆弧的中点，计算体积得到B正确；反证法证明AB与CD不垂直C正确；根据C选项知D错误，得到答案。

    因为，所以A正确；

    当，A，C各在所在圆弧的中点，此时三棱锥的底面BCD的面积和高均处于最大位置，此时体积为，所以B正确；

    AB与CD显然异面，用反证法证明他们不垂直．若，过A作BD的垂线，垂足为E，因为为直二面角，所以AE⊥平面BCD，所以，所以，所以，这与矛盾，所以AB与CD不垂直，所以C正确；

    假设存在一个位置，使得平面平面，过作于，则平面由于平面，与选项矛盾.

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，平面四边形中，,,,，将三角形沿翻折到三角形的位置，平面平面，为中点.

    （Ⅰ）求证：；

    （Ⅱ）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，倾斜角为60°的直线与椭圆分别交于A、B两点且，点C是椭圆上不同于A、B一点，则△ABC面积的最大值为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某港口某天0时至24时的水深（米）随时间（时）变化曲线近似满足如下函数模型（）.若该港口在该天0时至24时内，有且只有3个时刻水深为3米，则该港口该天水最深的时刻不可能为（ ）

    A.16时B.17时C.18时D.19时

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    (1)讨论f(x)的单调性；

    (2)若恰有两个极值点，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】点是曲线：上的一个动点，曲线在点处的切线与轴、轴分别交于，两点，点是坐标原点，①；②的面积为定值；③曲线上存在两点，使得是等边三角形；④曲线上存在两点，使得是等腰直角三角形，其中真命题的个数是（ ）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，侧棱底面，，，，，点在棱上，且.

    (1)证明：平面；

    (2)求平面与平面所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题：

    ①若将一组样本数据中的每个数据都加上同一个常数后，则样本的方差不变；

    ②在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高；

    ③设随机变量服从正态分布，若，则；

    ④对分类变量与的随机变量的观测值来说，越小，判断“与有关系”的把握越大.其中正确的命题序号是（ ）

    A.①②B.①②③C.①③④D.②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于定义在上的函数，若函数满足：①在区间上单调递减；②存在常数，使其值域为，则称函数为的“渐近函数”.

    （1）设，若在上有解，求实数取值范围；

    （2）证明：函数是函数，的渐近函数，并求此时实数的值；

    （3）若函数，，，证明：当时，不是的渐近函数.

    查看答案和解析>>

    同步练习册答案