
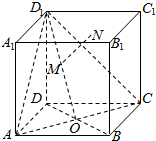
 如图所示,正方体ABCD-A1B1C1D1的棱长为1,BD∩AC=O,M是线段D1O上的动点,过点M作平面ACD1的垂线交平面A1B1C1D1于点N,则点N到点A距离的最小值为$\frac{\sqrt{6}}{2}$.
如图所示,正方体ABCD-A1B1C1D1的棱长为1,BD∩AC=O,M是线段D1O上的动点,过点M作平面ACD1的垂线交平面A1B1C1D1于点N,则点N到点A距离的最小值为$\frac{\sqrt{6}}{2}$. 分析 根据正方体的结构特征,可证,N在B1D1上,过N作NG⊥A1B1,交A1B1于G,设NG=x,利用勾股定理构造关于x的函数,求函数的最小值.
解答  解:∵平面ACD1⊥平面BDD1B1,又MN⊥平面ACD1,
解:∵平面ACD1⊥平面BDD1B1,又MN⊥平面ACD1,
∴MN?平面BDD1B1,∴N∈B1D1,
过N作NG⊥A1B1,交A1B1于G,将平面A1B1C1D1展开,如图:
设NG=x,(0≤x≤1),
∴AN=$\sqrt{{1}^{2}+(1-x)^{2}+{x}^{2}}$=$\sqrt{2{x}^{2}-2x+2}$=$\sqrt{2(x-\frac{1}{2})^{2}+\frac{3}{2}}$≥$\frac{\sqrt{6}}{2}$,
当x=$\frac{1}{2}$时,AN取最小值$\frac{\sqrt{6}}{2}$.
故答案为:$\frac{{\sqrt{6}}}{2}$.
点评 本题考查了正方体的结构性质,考查了函数思想的应用,构造函数模型,利用二次函数求最小值是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com