
���� �ɿ����������ߵĽ��뾶��ʽ����Բ�Ľ��뾶��ʽ��������ͨ����������������Բ���̣�����������꣬�ɵ�A��B��ĺ����귶Χ�������ý��뾶��ʽת��Ϊ��B��ĺ�����Ϊ������ʽ�ӣ��ٸ���ǰ�������B������귶Χ���㼴�ɣ�
���  �⣺����Բ���̺������߷�������
�⣺����Բ���̺������߷�������
���x0=$\frac{4}{3}$��y0=��$\sqrt{\frac{32}{3}}$��
����f��x��=$\left\{\begin{array}{l}{2\sqrt{2x}��0��x��\frac{4}{3}}\\{\frac{\sqrt{3}}{2}\sqrt{16-{x}^{2}}��\frac{4}{3}��x��4}\end{array}\right.$��
ֱ��y=a��0��a��$\sqrt{\frac{32}{3}}$����
��������y=f��x����ֱ��y=a��ͼ��
��ͼ��ɵ�A���������ϣ�B����Բ�ϣ�
�ɽ��뾶��ʽ�ɵã���ABN���ܳ�Ϊ
|AN|+|BN|+|AB|=xA+$\frac{p}{2}$+a-exB+xB-xA
=2+4-$\frac{1}{2}$xB+xB=6+$\frac{1}{2}$xB��
��xB�ʣ�$\frac{4}{3}$��4����
�ɵ�6+$\frac{1}{2}$xB�ʣ�$\frac{20}{3}$��8����
�ʡ�ABN���ܳ���ȡֵ��Χ�ǣ�$\frac{20}{3}$��8����
�ʴ�Ϊ����$\frac{20}{3}$��8����
���� ������Ҫ����������������Բ���뾶��ʽ��Ӧ�ã�����ʱҪ���ڰ�δ֪ת��Ϊ��֪�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
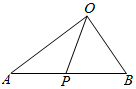 ��ͼ���ڡ�AOB�У���P��AB�ϣ���$\overrightarrow{OP}$=m$\overrightarrow{PA}$+2m$\overrightarrow{OB}$��m��R������$\frac{|\overrightarrow{PA}|}{|\overrightarrow{PB}|}$��ֵ��
��ͼ���ڡ�AOB�У���P��AB�ϣ���$\overrightarrow{OP}$=m$\overrightarrow{PA}$+2m$\overrightarrow{OB}$��m��R������$\frac{|\overrightarrow{PA}|}{|\overrightarrow{PB}|}$��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 8 | C�� | 13 | D�� | 18 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
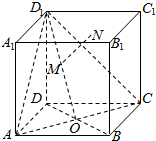 ��ͼ��ʾ��������ABCD-A1B1C1D1���ⳤΪ1��BD��AC=O��M���߶�D1O�ϵĶ��㣬����M��ƽ��ACD1�Ĵ��߽�ƽ��A1B1C1D1�ڵ�N�����N����A�������СֵΪ$\frac{\sqrt{6}}{2}$��
��ͼ��ʾ��������ABCD-A1B1C1D1���ⳤΪ1��BD��AC=O��M���߶�D1O�ϵĶ��㣬����M��ƽ��ACD1�Ĵ��߽�ƽ��A1B1C1D1�ڵ�N�����N����A�������СֵΪ$\frac{\sqrt{6}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com