
分析 (1)由$\overrightarrow{a}$⊥$\overrightarrow{b}$,可得12+5cosα•(-4tanα)=0,利用同角三角函数基本关系式可求sinα,进而可求cosα,tanα的值,从而解得$\overrightarrow{a}$=(4,4),$\overrightarrow{b}$=(3,-3),可得$\overrightarrow{a}+\overrightarrow{b}$=(7,1),即可计算得解|$\overrightarrow{a}$⊥$\overrightarrow{b}$|的值.
(2)由(1)及二倍角公式可得sin2α,即可计算求值.
解答 解:(1)∵$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=0,
即12+5cosα•(-4tanα)=0,
解得sinα=$\frac{3}{5}$,
又α∈(0,$\frac{π}{2}$),
∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{4}{5}$,
∴tanα=$\frac{sinα}{cosα}$=$\frac{3}{4}$,
∴$\overrightarrow{a}$=(4,4),$\overrightarrow{b}$=(3,-3),
∴$\overrightarrow{a}+\overrightarrow{b}$=(7,1),
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=5$\sqrt{2}$.
(2)∵由(1)可得sin2α=2sinαcosα=$\frac{24}{25}$,
∴$\frac{2sinαcosα}{sinα+cosα-1}$=$\frac{\frac{24}{25}}{\frac{3}{5}+\frac{4}{5}-1}$=$\frac{12}{5}$.
点评 本题主要考查了平面向量数量积的运算,同角三角函数基本关系式在三角函数求值中的应用,考查了转化思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 椭圆 | C. | 直线 | D. | 以上都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p为假命题;¬p:?x∈(0,π),x>sinx | B. | 命题p为假命题;¬p:?x∈(0,π),x≤sinx | ||
| C. | 命题p为真命题;¬p:?x∈(0,π),x≤sinx | D. | 命题p为真命题;¬p:?x∈(0,π),x≤sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
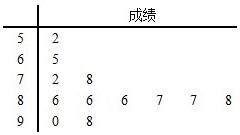 为落实国务院“十三五”规划中的社会民生建设,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式如图:根据老年人体质健康标准,成绩不低于80的为优良.
为落实国务院“十三五”规划中的社会民生建设,某医院到社区检查老年人的体质健康情况.从该社区全体老年人中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式如图:根据老年人体质健康标准,成绩不低于80的为优良.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com