练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．已知a＞b，a-$\frac{1}{a}$＞b-$\frac{1}{b}$同时成立，则a，b应满足的条件是ab＞0或ab＜-1．．

    分析 由a＞b，a-$\frac{1}{a}$＞b-$\frac{1}{b}$同时成立得到$\frac{1}{ab}$＞-1，通过讨论ab的符号，求出答案即可．

    解答 解：∵a-$\frac{1}{a}$＞b-$\frac{1}{b}$，
    a-b＞$\frac{1}{a}$-$\frac{1}{b}$=-$\frac{a-b}{ab}$ ①
    ∵a-b＞0，
    所以由 ①两边同除a-b得
    ∴$\frac{1}{ab}$＞-1 ②
    下面分别讨论
    （1）当ab＞0（同号）时，②式恒成立
    （2）当ab＜0（异号）时，要使②式成立，必须使ab＜-1
    综合（1）（2）
    可知ab应满足的条件是ab＞0 或ab＜-1，
    故答案为：ab＞0或ab＜-1．

    点评 本题考查了不等式的基本性质，考查转化思想，分类讨论思想，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．设关于x、y的不等式组$\left\{\begin{array}{l}{2x-y+1＞0}\\{3x-2＜0}\\{y-a＞0}\end{array}\right.$表示的平面区域内存在点P（x0，y0），满足x0-2y0=2，则a的取值范围是（　　）
    A．（-∞，-$\frac{5}{3}$）B．（-∞，-$\frac{2}{3}$）C．（-∞，$\frac{1}{3}$）D．（-∞，$\frac{4}{3}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知向量$\overrightarrow{m}$=（sinωx，sin（ωx+$\frac{π}{6}$）），$\overrightarrow{n}$=（cosωx，sinωx），其中ω＞0，f（x）=$\overrightarrow{m}$$•\overrightarrow{n}$．
    （1）求函数f（x）的值域；
    （2）若f（$\frac{π}{6}$）=f（$\frac{π}{2}$），且f（x）的图象在（$\frac{π}{6}$，$\frac{π}{2}$）内有最高点但无最低点，求ω的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知函数$y=2sin（2x+φ）（|φ|＜\frac{π}{2}）$的图象经过点（0，-1），则该函数的一个单调递增区间为（　　）
    A．[-$\frac{π}{6}$，$\frac{π}{3}$]B．[$\frac{π}{3}$，$\frac{5π}{6}$]C．[-$\frac{5π}{12}$，$\frac{π}{12}$]D．[$\frac{π}{12}$，$\frac{7π}{12}$]]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的解析式为f（x）=2sin（$\frac{π}{3}$x+$\frac{π}{6}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

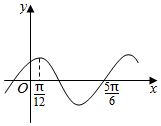    2．设函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0），且函数f（x）的部分图象如图所示，则有（　　）
    A．f（-$\frac{3π}{4}$）＜f（$\frac{5π}{3}$）＜f（$\frac{7π}{6}$）B．f（-$\frac{3π}{4}$）＜f（$\frac{7π}{6}$）＜f（$\frac{5π}{3}$）C．f（$\frac{5π}{3}$）＜f（$\frac{7π}{6}$）＜f（-$\frac{3π}{4}$）D．f（$\frac{5π}{3}$）＜f（-$\frac{3π}{4}$）＜f（$\frac{7π}{6}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．设集合A={-1，0，1}，B={a-1，a+$\frac{1}{a}}$}，A∩B={0}，则实数a的值为1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知$\overrightarrow{a}$=（4，5cosα），$\overrightarrow{b}$=（3，-4tanα），α∈（0，$\frac{π}{2}$），且$\overrightarrow{a}$⊥$\overrightarrow{b}$；
    （1）求|$\overrightarrow{a}$$+\overrightarrow{b}$|；
    （2）求$\frac{2sinαcosα}{sinα+cosα-1}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知向量$\overrightarrow{a}$=（2cosα，2sinα），$\overrightarrow{b}$=（sinβ，cosβ）．
    （1）求|$\overrightarrow{a}$$+\overrightarrow{b}$|的最小值；
    （2）若向量$\overrightarrow{c}$=（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），且$\overrightarrow{b}$$•\overrightarrow{c}$=$\frac{3}{5}$，β∈（0，π），求sinβ的值．

    查看答案和解析>>

    同步练习册答案