
(本题满分12分)如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.
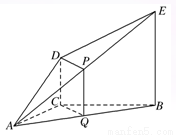
(1)证明:PQ∥平面ACD;
(2)求AD与平面ABE所成角的正弦值.
(1)见解析;(2)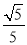
【解析】
试题分析:(1)证明:因为P,Q分别为AE,AB的中点,
所以PQ∥EB.又DC∥EB,因此PQ∥DC,
又PQ?平面ACD,
从而PQ∥平面ACD.
(2)如图,
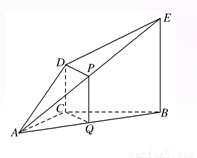
连接CQ,DP,因为Q为AB的中点,且AC=BC,所以CQ⊥AB.
因为DC⊥平面ABC,
EB∥DC,
所以EB⊥平面ABC,因此CQ⊥EB.[来
故CQ⊥平面ABE.
由(1)有PQ∥DC,又PQ=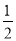 EB=DC,
EB=DC,
所以四边形CQPD为平行四边形,故DP∥CQ.
因此DP⊥平面ABE,∠DAP为AD和平面ABE所成的角,
在Rt△DPA中,AD=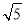 ,DP=1,
,DP=1,
sin∠DAP=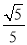 ,
,
因此AD和平面ABE所成角的正弦值为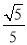 .
.
考点:本题考查集合的交集,并集的运算,集合与集合的关系


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源:2014-2015学年广东省汕头市高三上学期第三次段考理科数学试卷(解析版) 题型:选择题
已知离散型随机变量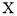 的分布列为
的分布列为
|
|
|
|
|
|
|
|
则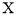 的数学期望
的数学期望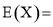 ( )
( )
A.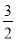 B.
B.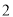 C.
C. D.
D.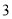
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东三水区实验中学高二上学期第五段测文科数学试卷(解析版) 题型:选择题
如果直线ax+2y+1=0与3x-y=0平行,那么系数a=( )
A.–3 B.–6 C.–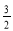 D.
D.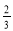
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东三水区实验中学高二上学期第五段测理科数学试卷(解析版) 题型:选择题
过点(1,2),且在两坐标轴上的截距相等的直线有( )
A.1条 B.2条 C.3条 D.4条
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东三水区实验中学高二上学期第五段测理科数学试卷(解析版) 题型:选择题
如图是某几何体的三视图,则这个几何体是( )

A.圆柱 B.球
C.圆锥 D.棱柱
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省天水市高三第五次检测文科数学试卷(解析版) 题型:填空题
第十二届全运会于2013年8月31日在沈阳举行,运动会期间从自A大学的2名志愿者和自B大学的4名志愿者中随机抽取2人到体操比赛场馆服务,至少有一名A大学志愿者的概率是_______.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省天水市高三第五次检测文科数学试卷(解析版) 题型:填空题
第十二届全运会于2013年8月31日在沈阳举行,运动会期间从自A大学的2名志愿者和自B大学的4名志愿者中随机抽取2人到体操比赛场馆服务,至少有一名A大学志愿者的概率是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com