
【题目】如图,已知在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() =60°,沿
=60°,沿![]() ,
,![]() 折成三棱柱
折成三棱柱![]() .
.

(1)若![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求证:
的中点,求证:![]() ∥平面
∥平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值
的余弦值
【答案】(1)见解析;(2)![]()
【解析】
分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,在三角形
,在三角形![]() 中,得到
中,得到![]() ,证得
,证得![]() 平面
平面![]() ,又由
,又由![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点证得
的中点证得![]() 平面
平面![]() ,即可证得面
,即可证得面![]() 平面
平面![]() ,利用面面平行的性质,即可得到
,利用面面平行的性质,即可得到![]() 平面
平面![]() .
.
(2)建立如图所示的空间直角坐标系,求得平面![]() 和平面
和平面![]() 的法向量,利用向量的夹角公式,即可求解二面角
的法向量,利用向量的夹角公式,即可求解二面角![]() 的余弦值.
的余弦值.
详解:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,在三角形
,在三角形![]() 中,
中,
∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
由于![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,由棱柱的性质可得
的中点,由棱柱的性质可得![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
∴平面![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)连接![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,又
,又![]() 且
且![]() ,
,
∴![]() 平面
平面![]() .
.
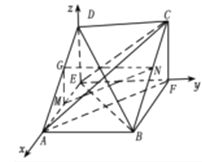
建立如图所示的空间直角坐标系,
可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则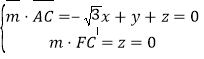 ,则
,则![]() ,令
,令![]() ,
,
得![]() ,则
,则![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设平面![]() 的法向量为
的法向量为![]() ,则
,则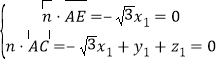 ,
,
则![]() ,令
,令![]() ,得
,得![]() ,
,
∴![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设![]() ,
,![]() 所成角为
所成角为![]() ,则
,则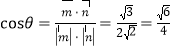 ,
,
由图可知二面角![]() 的余弦值为
的余弦值为![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】某公司生产甲、乙两种产品所得利润分别为![]() 和
和![]() (万元),它们与投入资金(万元)的关系有经验公式
(万元),它们与投入资金(万元)的关系有经验公式![]() ,
,![]() .今将120万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投资金额都不低于20万元.
.今将120万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投资金额都不低于20万元.
(Ⅰ)设对乙产品投入资金![]() 万元,求总利润
万元,求总利润![]() (万元)关于
(万元)关于![]() 的函数关系式及其定义域;
的函数关系式及其定义域;
(Ⅱ)如何分配使用资金,才能使所得总利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(10分)四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.

(1)求四面体ABCD的体积;
(2)证明:四边形EFGH是矩形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 在椭圆上(异于椭圆
在椭圆上(异于椭圆![]() 的左、右顶点),过右焦点
的左、右顶点),过右焦点![]() 作∠
作∠![]() 的外角平分线
的外角平分线![]() 的垂线
的垂线![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() (
(![]() 为坐标原点),椭圆的四个顶点围成的平行四边形的面积为
为坐标原点),椭圆的四个顶点围成的平行四边形的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,求当三角形
,求当三角形![]() 的面积最大时,直线
的面积最大时,直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com