
分析 (1)当a=2时,利用导数即可判断函数f(x)的单调性.
(2)a=4,先求导,再根据基本不等式得到f′(x)≥4$\sqrt{2}$-6,不存在6x+y+m=0这类直线的切线,存在3x-y+n=0这类直线的切线
(3)问题等价于y=g(x)=$\frac{{2x}_{0}^{2}-6{x}_{0}+4}{{x}_{0}}$(x-x0)+x02-6x0+4lnx0,令$ϕ(x)={x_0}{x^2}-(2{x^2}_0+4)x+4lnx•{x_0}+x_0^3+4{x_0}-4ln{x_0}•{x_0}$,由此入手,能够求出一个“类对称点”的横坐标.
解答 解:(1)函数f(x)的定义域是(0,+∞).
∵f(x)=x2-4x+2lnx,
∴$f'(x)=2x-4+\frac{2}{x}=\frac{{2{x^2}-4x+2}}{x}=\frac{{2{{(x-1)}^2}}}{x}≥0$
∵f'(x)>0在定义域(0,+∞)内恒成立,
∴函数f(x)在(0,+∞)都是单调递增.
(2)当a=4时,f(x)=x2-6x+4lnx,
则$f'(x)=\frac{{2{x^2}-6x+4}}{x}$,
∵x>0,
∴$f'(x)=2(x+\frac{2}{x}-3)≥4\sqrt{2}-6$.
∴曲线f(x)在定义域内的任意一点处的切线斜率都大于或等于$4\sqrt{2}-6$,
而$3∈[{4\sqrt{2}-6,+∞}]$,
∴曲线f(x)可以与3x-y+n=0中的一条直线相切,另一组直线无切线.
此时切线的斜率是3,对应的切线方程式y=3x-20+8ln2或$y=3x-\frac{17}{4}-4ln2$;
(3)由(2)得函数y=f(x)在点P(x0,f(x0))处的切线方程为
l:y=g(x)=$\frac{{2x}_{0}^{2}-6{x}_{0}+4}{{x}_{0}}$(x-x0)+x02-6x0+4lnx0.
若函数f(x)=x2-6x+4lnx存在“类对称点”P(x0,f(x0)),
则等价与当0<x<x0时,f(x)<g(x),当x<x0时,f(x)>g(x)恒成立,
①当0<x<x0时,f(x)<g(x),恒成立,
等价于当0<x<x0时,${x^2}-6x+4lnx<\frac{{2{x^2}_0-6{x_0}+4}}{x_0}(x-{x_0})+{x^2}_0-6{x_0}+4ln{x_0}$恒成立,
即当0<x<x0时,${x_0}{x^2}-(2{x^2}_0+4)x+4{x_0}•lnx+{x^3}_0+4{x_0}-4{x_0}•ln{x_0}<0$恒成立.
令$ϕ(x)={x_0}{x^2}-(2{x^2}_0+4)x+4lnx•{x_0}+x_0^3+4{x_0}-4ln{x_0}•{x_0}$,
则ϕ(x0)=0,要使ϕ(x)<0在0<x<x0恒成立,只要ϕ(x)在(0,x0)单调递增即可.
又∵$ϕ'(x)=2{x_0}x-(2{x^2}_0+4)+\frac{{4{x_0}}}{x}=\frac{{2(x{\;}_0x-2)(x-{x_0})}}{x}$,
∴${x_0}≤\frac{2}{x_0}$,即$0<{x_0}≤\sqrt{2}$.
②同理当x>x0时,f(x)>g(x)恒成立,${x_0}≥\sqrt{2}$,
∴${x_0}=\sqrt{2}$.
∴y=f(x)存在“类对称点”,其中一个“类对称点”的横坐标是${x_0}=\sqrt{2}$.
点评 本题考查函数的单调区间的求法,考查类对称点的求法.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,注意导数性质的灵活运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
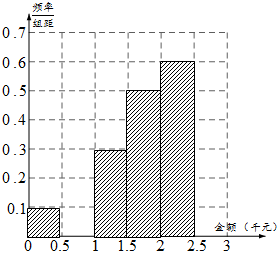 某网络营销部门为了统计某市网友“双11”在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图):
某网络营销部门为了统计某市网友“双11”在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图):| 网购金额 (单位千元) | 频数 | 频率 |
| (0,0.5] | 3 | 0.05 |
| (0.5,1] | x | p |
| (1,1.5] | 9 | 0.15 |
| (1.5,2] | 15 | 0.25 |
| (2,2.5] | 18 | 0.30 |
| (2.5,3] | y | q |
| 合计 | 60 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
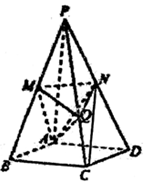 如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分别为PB,PD的中点.
如图,在四棱锥P-ABCD中,底面是边长为2$\sqrt{3}$的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=2$\sqrt{6}$,M、N分别为PB,PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{8}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com