
分析 (1)通过讨论x的范围,求出各个区间上的x的范围,取并集即可;
(2)求出f(x)的最小值,问题转化为$lo{g}_{\frac{1}{3}}(m-3)$≤-3,解出即可.
解答 解:(1)x≥2时:f(x)=x-2-x-1=-3<1,成立,
-1<x<2时:f(x)=2-x-x-1=1-2x<1,解得:0<x<2,
x≤-1时:f(x)=2-x+x+1=3<1不成立,
故不等式的解集是(0,+∞);
(Ⅱ)由(1)可知f(x)的最小值是-3,
若$?x∈R,f(x)≥{log_{\frac{1}{3}}}(m-3)$,
即有f(x)min≥$lo{g}_{\frac{1}{3}}(m-3)$,
即有$lo{g}_{\frac{1}{3}}(m-3)$≤-3,解得:m≥30,
则实数m的取值范围为[30,+∞).
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 4+20π | B. | 16+12π | C. | 16+16π | D. | 16+20π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
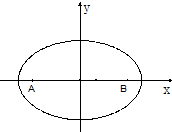 椭圆满足这样的光学性质:从椭圆的一个焦点发射的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现有一个水平放置的椭圆形台球盘,满足方程$\frac{x^2}{64}+\frac{y^2}{28}=1$,点A,B是它的两个焦点.当静止的小球从点A开始出发,沿直线运动,经椭圆壁反射后再回到点A时,此时小球经过的路程可能是( )
椭圆满足这样的光学性质:从椭圆的一个焦点发射的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点.现有一个水平放置的椭圆形台球盘,满足方程$\frac{x^2}{64}+\frac{y^2}{28}=1$,点A,B是它的两个焦点.当静止的小球从点A开始出发,沿直线运动,经椭圆壁反射后再回到点A时,此时小球经过的路程可能是( )| A. | 32或4或$16-4\sqrt{7}$ | B. | $16+4\sqrt{7}$或28或$16-4\sqrt{7}$ | ||
| C. | 28或4或$16+4\sqrt{7}$ | D. | 32或28或4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com