
| A�� | �٢� | B�� | �ڢ� | C�� | �٢� | D�� | �ڢ� |
���� ������֪�ɵ�sin2��+sin2����+�ȣ�=1���ã�$\frac{��}{2}$+��+��+2k��=0�����+��+2k��=$\frac{��}{2}$��k��Z���������жϦȺͦÿ����ǹ��廥�ࣻ
������sin��=sin����-$\frac{��}{2}$������æ�-��=2k��-$\frac{��}{2}$�����+��=2k��+$\frac{3��}{2}$�����ɵý�Ⱥͦò������ǹ��廥�ࣻ
�۽�á�sin��=sin��$\frac{��}{2}$-�ã�����sin��=sin��$\frac{��}{2}$-�ã�ʱ���ɵæ�=$\frac{��}{2}$-��+2k�У���k��Z�����ɵ�a�ͦ��п����ǹ��廥�ࣻ
�ܽ��cos2��+sin2��=1���ɵæ�-��=2k�У��ɵæúͦȲ������ǹ��廥�࣮
��� �⣺��sin����+�ȣ�=-$\frac{1}{3}$���ɵã�sin��=$\frac{1}{3}$��
���sin2��+sin2����+�ȣ�=1���ɵã�$\frac{��}{2}$+��+��+2k��=0�����+��+2k��=$\frac{��}{2}$��k��Z�����ʦȺͦÿ����ǹ��廥�ࣻ
��cos����+�ã�=-cos��=-sin����+�ȣ�=sin��=sin����-$\frac{��}{2}$����
���=��-$\frac{��}{2}$+2k�����=��-����-$\frac{��}{2}$��+2k����k��Z����
���-��=2k��-$\frac{��}{2}$�����+��=2k��+$\frac{3��}{2}$����k��Z����
��+�²����ܵ���90�㣬�Ⱥͦò������ǹ��廥�ࣻ
�۵�tan��=-2$\sqrt{2}$ʱ���ɵ�cos��=��$\frac{1}{3}$=��sin��=sin��$\frac{��}{2}$-�ã���
��sin��=sin��$\frac{��}{2}$-�ã�ʱ���ɵæ�=$\frac{��}{2}$-��+2k�У���k��Z����
�ɵ�a�ͦ��п����ǹ��廥�ࣻ
�ܵ�tan��=$\frac{\sqrt{2}}{4}$ʱ��cos��=��$\frac{2\sqrt{2}}{3}$����ʱcos2��+sin2��=1����-��=2k�У���k��Z����
��úͦȲ������ǹ��廥�࣮
��ѡ��C��
���� ������Ҫ���������Ǻ����յ���ʽ�����ã����������Ǻ�����ͼ������ʣ�������ѧ�������ͽ������������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�������и���������Ӧ�Կ���һ��ѧ�Ծ��������棩 ���ͣ�ѡ����
��֪ʵ�� ����
����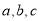 �Ĵ�С��ϵΪ�� ��
�Ĵ�С��ϵΪ�� ��
A��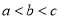 B��
B��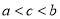
C��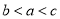 D��
D��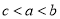
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʯ����һ�и���9���¿���ѧ���ģ��Ծ��������棩 ���ͣ�ѡ����
���������ĸ����⣺
��1����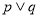 Ϊ�����⣬��
Ϊ�����⣬��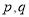 ��Ϊ�����⣻
��Ϊ�����⣻
��2�����⡰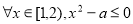 ��Ϊ�������һ����ֲ���Ҫ����������
��Ϊ�������һ����ֲ���Ҫ����������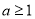 ��
��
��3����֪����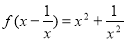 ����
����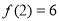 ��
��
��4��������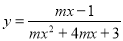 �Ķ�����Ϊ
�Ķ�����Ϊ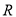 ����ʵ��
����ʵ��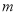 ��ȡֵ��Χ��
��ȡֵ��Χ��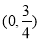 ��
��
����������ĸ����ǣ� ��
A��0 B��1 C��2 D��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{3}$ | B�� | 2 | C�� | 4 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 8 | C�� | 9 | D�� | 10 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com