
分析 (Ⅰ)由向量和三角函数运算可得cosA,可得角A;
(Ⅱ)由余弦定理可得bc的方程,结合b+c=4可解得b和c,代入三角形的面积公式可得.
解答 解:(Ⅰ)∵$\overrightarrow m$=(-cos$\frac{A}{2}$,sin$\frac{A}{2}$),$\overrightarrow n$=(cos$\frac{A}{2}$,sin$\frac{A}{2}$),且$\overrightarrow m•\overrightarrow n$=$\frac{1}{2}$.
∴$\overrightarrow m•\overrightarrow n$=-cos2$\frac{A}{2}$+sin2$\frac{A}{2}$=-cosA=$\frac{1}{2}$,∴cosA=-$\frac{1}{2}$,
又∵A∈(0°,180°),∴A=120°;
(Ⅱ)由余弦定理得a2=b2+c2-2bccos120°即b2+c2+bc=12,
又∵b+c=4,∴联立方程$\left\{\begin{array}{l}{b^2}+{c^2}+bc=12\\ b+c=4\end{array}\right.$,
解得$\left\{\begin{array}{l}b=2\\ c=2\end{array}\right.$,∴S△ABC=$\frac{1}{2}$bcsin120°=$\sqrt{3}$.
点评 本题考查正余弦定理解三角形,涉及向量的知识和三角形的面积公式,属基础题.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源:2017届重庆市高三理上适应性考试一数学试卷(解析版) 题型:选择题
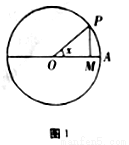
如图1,圆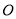 的半径为1,
的半径为1,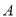 是圆上的定点,
是圆上的定点,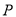 是圆上的动点,角
是圆上的动点,角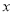 的始边为射线
的始边为射线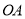 ,终边为射线
,终边为射线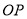 ,过点
,过点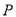 作直线
作直线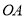 的垂线,垂足为
的垂线,垂足为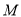 ,将点
,将点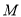 到直线
到直线 的距离与
的距离与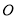 到
到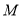 的距离之和表示成
的距离之和表示成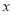 的函数
的函数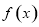 ,则
,则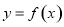 在
在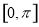 上的图象大致是( )
上的图象大致是( )
A.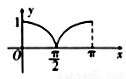 B.
B.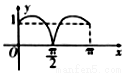
C.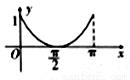 D.
D.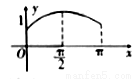
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
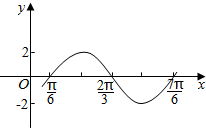
| A. | ω=2,φ=-$\frac{π}{3}$ | B. | ω=2,φ=$\frac{π}{3}$ | C. | ω=2,ω=-$\frac{π}{6}$ | D. | ω=1,φ=$\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com