
分析 根据方程的根与对应函数的零点的关系,我们可用图象法解答本题,即关于x的方程$\sqrt{4-{x^2}}-kx+2k-3=0$有两个不同的实数根,则函数y=$\sqrt{4-{x}^{2}}$的图象与y=kx+3-2k的图象有且只有两个交点,在同一坐标系中画出函数y=$\sqrt{4-{x}^{2}}$的图象与y=kx+3-2k的图象,分析图象即可得到答案
解答 解:若关于x的方程$\sqrt{4-{x}^{2}}$-kx-3+2k=0有且只有两个不同的实数根,
则函数y=$\sqrt{4-{x}^{2}}$的图象与y=kx+3-2k的图象有且只有两个交点
∵函数y=kx+3-2k的图象恒过(2,3)点
故在同一坐标系中画出函数y=$\sqrt{4-{x}^{2}}$的图象与y=kx+3-2k的图象如下图所示:
由图可知
当k=$\frac{5}{12}$时,直线与圆相切,
当k=$\frac{3}{4}$时,直线过半圆的左端点(-2,0)
若函数y=$\sqrt{4-{x}^{2}}$的图象与y=kx+3-2k的图象有且只有两个交点,则$\frac{5}{12}$<k≤$\frac{3}{4}$
故答案为:$\frac{5}{12}$<k≤$\frac{3}{4}$.
点评 本题考查的知识点是根的存在性及根的个数判断,方程的根与函数零点的关系,函数的图象,其中在确定无法解答的方程问题时,将其转化为确定对应函数的零点,利用数形结合解答是最常用的方法.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
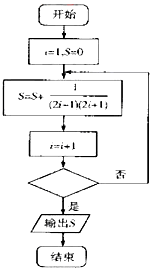
| A. | i>2014 | B. | i>2014 | C. | i>2015 | D. | i>2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 把正整数按一定的规则排成了如图所示的三角形数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,如a63=18,若aij=2012,则i+j=( )
把正整数按一定的规则排成了如图所示的三角形数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行,从左往右数第j个数,如a63=18,若aij=2012,则i+j=( )| A. | 75 | B. | 76 | C. | 77 | D. | 78 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com