
分析 先根据奇函数的定义求出a=$\frac{1}{2}$,再分别根据充分条件和必要条件的定义判断即可.
解答 解:∵$f(x)=\frac{1}{{{3^x}-1}}+a$,
∴f(-x)=$\frac{1}{{3}^{-x}-1}$+a,
∵函数f(x)为奇函数,
∴f(-x)=-f(x),
∴$\frac{1}{{3}^{-x}-1}$+a=-$\frac{1}{{3}^{x}-1}$-a,
∴a=$\frac{1}{2}$,
∵f(-1)=-1,
∴$\frac{1}{{3}^{-1}-1}$+a=-1,
解得a=$\frac{1}{2}$,
“f(-1)=-1”是“函数f(x)为奇函数”的充要条件,
故答案为:充要.
点评 本题考查了充要条件和奇函数的定义和性质,属于基础题.


科目:高中数学 来源: 题型:解答题
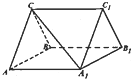 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 60° | C. | 90° | D. | 135° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com