
分析 设|MF1|=m,|MF2|=n,不妨设m>n.可得:m+n=2a1,m-n=2a2,(2c)2=m2+n2-2mncos60°=(m+n)2-2mn-2mncos60°,化简基础即可得出.
解答 解:设|MF1|=m,|MF2|=n,不妨设m>n.
则m+n=2a1,m-n=2a2,(2c)2=m2+n2-2mncos60°=(m+n)2-2mn-2mncos60°,
可得:4c2=${a}_{1}^{2}$+12${a}_{2}^{2}$,
∴4=$(\frac{1}{\sqrt{2}})^{2}$+12×$\frac{1}{{e}^{2}}$,解得e=$\frac{2\sqrt{42}}{7}$.
故答案为:$\frac{2\sqrt{42}}{7}$.
点评 本题考查了椭圆与双曲线的定义标准方程及其性质、余弦定理,考查了推理能力与计算能力,属于中档题.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=1-x2 | B. | $y={log_{\frac{1}{2}}}x$ | C. | $y={x^{\frac{1}{2}}}$ | D. | $y={(\frac{1}{3})^x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
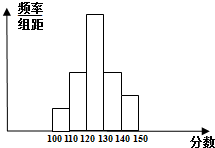 为了了解学生的数学复习情况,某校从第四次模拟考试成绩中抽取一个样本,将样本分成5组,绘成频率分布直方图,图中从左到右小矩形面积之比为2:5:10:5:3,最左边一组的频数为4,请结合直方图解决下列问题.
为了了解学生的数学复习情况,某校从第四次模拟考试成绩中抽取一个样本,将样本分成5组,绘成频率分布直方图,图中从左到右小矩形面积之比为2:5:10:5:3,最左边一组的频数为4,请结合直方图解决下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com