
| x | 1 | 2 | 3 | 4 | 5 |
| y | 5 | 6 | 7 | 8 | 10 |
| A. | 26.2 | B. | 27 | C. | 27.6 | D. | 28.2 |
分析 根据所给的数据求出这组数据的横标和纵标的平均数,即这组数据的样本中心点,根据样本中心点在线性回归直线上,把样本中心点代入求出a的值,写出线性回归方程,代入x的值,预报出结果.
解答 解:∵由表格可知$\overline{x}$=3,$\overline{y}$=7.2,
∴这组数据的样本中心点是(3,7.2),
根据样本中心点在线性回归直线上,
∴7.2=a+1.2×3,
∴a=3.6,
∴这组数据对应的线性回归方程是y=1.2x+3.6,
∵x=20,
∴y=1.2×20+3.6=27.6.
故选:C.
点评 本题考查线性回归方程,考查样本中心点,做本题时要注意本题把利用最小二乘法来求线性回归方程的系数的过程省掉,只要求a的值,这样使得题目简化,注意运算不要出错.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
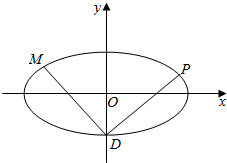 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,3,4} | B. | {2,3,4,5} | C. | {1,2,3,4,5} | D. | {-2,1,2,3,4,5} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com