
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.
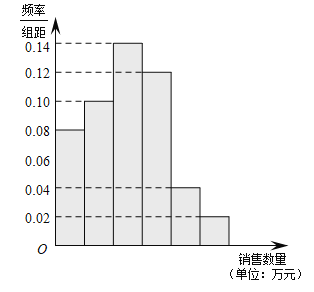
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益y(单位:万元) | 1 | 3 | 4 | 7 |
表中的数据显示,x与y之间存在线性相关关系,请将(2)的结果填入上表的空白栏,并计算y关于x的回归方程.
回归直线的斜率和截距的最小二乘法估计公式分别为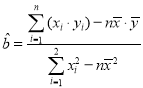 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】某超市从现有甲、乙两种酸奶的日销售量(单位:箱)的1200个数据(数据均在区间![]() 内)中,按照
内)中,按照![]() 的比例进行分层抽样,统计结果按
的比例进行分层抽样,统计结果按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,分组,整理如下图:
,分组,整理如下图:


(1)求频率分布直方图(图乙)中![]() 的值,并估计1200个日销售量中,数据在区间
的值,并估计1200个日销售量中,数据在区间![]() 中的个数.
中的个数.
(2)从日销售量在![]() 的甲种酸奶的数据样本中抽取3个,记在
的甲种酸奶的数据样本中抽取3个,记在![]() 内的数据个数为
内的数据个数为![]() ,求
,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四色猜想是世界三大数学猜想之一,1976年数学家阿佩尔与哈肯证明,称为四色定理.其内容是:“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域,每一个区域总可以用1,2,3,4四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为1,粗实线围城的各区域上分别标有数字1,2,3,4的四色地图符合四色定理,区域![]() 和区域
和区域![]() 标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为1的区域的概率所有可能值中,最大的是______.
标记的数字丢失.若在该四色地图上随机取一点,则恰好取在标记为1的区域的概率所有可能值中,最大的是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 和
和![]() 同时在
同时在![]() 处取得极小值,则称
处取得极小值,则称![]() 和
和![]() 为一对“
为一对“![]() 函数”.
函数”.
(1)试判断![]() 与
与![]() 是否是一对“
是否是一对“![]() 函数”;
函数”;
(2)若![]() 与
与![]() 是一对“
是一对“![]() 函数”.
函数”.
①求![]() 和
和![]() 的值;
的值;
②当![]() 时,若对于任意
时,若对于任意![]() ,恒有
,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱锥![]() 的底面边长和高都为2.现从该棱锥的5个顶点中随机选取3个点构成三角形,设随机变量
的底面边长和高都为2.现从该棱锥的5个顶点中随机选取3个点构成三角形,设随机变量![]() 表示所得三角形的面积.
表示所得三角形的面积.
(1)求概率![]() 的值;
的值;
(2)求随机变量![]() 的概率分布及其数学期望
的概率分布及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为 .
.
(1)求![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
,![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 中,
中,![]() ,对任意正整数
,对任意正整数![]() ,
, .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,请求出实数
是等比数列?若存在,请求出实数![]() 及公比q的值,若不存在,请说明理由;
及公比q的值,若不存在,请说明理由;
(3)求数列![]() 前n项和
前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑。若三棱锥P-ABC为鳖臑,PA⊥面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球的球面上,则球0的表面积为( )
A. 8πB. 12πC. 20πD. 24π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com