
(2014·黄冈模拟)如图,等腰梯形ABCD中,AB∥CD且AB=2,AD=1,DC=2x(x∈(0,1)).以A,B为焦点,且过点D的双曲线的离心率为e1;以C,D为焦点,且过点A的椭圆的离心率为e2,则e1+e2的取值范围为( )

A.[2,+∞) B.( ,+∞)
,+∞)
C. D.(
D.( +1,+∞)
+1,+∞)
科目:高中数学 来源:2014年高考数学人教版评估检测 第四章平面向量、数系扩充与复数引入(解析版) 题型:填空题
(2013·重庆高考)在OA为边,OB为对角线的矩形中,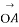 =(-3,1),
=(-3,1), =(-2,k),则实数k=________.
=(-2,k),则实数k=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第六章 不等式、推理与证明(解析版) 题型:填空题
(2014·黄冈模拟)已知a,b都是正实数,函数y=2aex+b的图象过(0,1)点,则 +
+ 的最小值是________.
的最小值是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第八章 平面解析几何(解析版) 题型:解答题
(2014·武汉模拟)已知点P是圆M:x2+(y+m)2=8(m>0,m≠ )上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
)上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
(1)当P在圆M上运动时,记动点Q的轨迹为曲线Г,判断曲线Г为何种曲线,并求出它的标准方程.
(2)过原点斜率为k的直线交曲线Г于A,B两点,其中A在第一象限,且它在x轴上的射影为点C,直线BC交曲线Г于另一点D,记直线AD的斜率为k′,是否存在m,使得对任意的k>0,都有|k·k′|=1?若存在,求m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第八章 平面解析几何(解析版) 题型:填空题
已知两条直线y=ax-2和y=(a+2)x+1互相垂直,则a等于________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第八章 平面解析几何(解析版) 题型:选择题
抛物线的顶点在坐标原点,焦点与双曲线 -
- =1的一个焦点重合,则该抛物线的标准方程可能是( )
=1的一个焦点重合,则该抛物线的标准方程可能是( )
A .x2=4y B.x2=-4y
.x2=4y B.x2=-4y
C.y2=-12x D.x2=-12y
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第五章 数列(解析版) 题型:解答题
已知数列{an}满足an+1= (n∈N*),且a1=
(n∈N*),且a1= .
.
(1)求证:数列 是等差数列,并求an.
是等差数列,并求an.
(2)令bn= (n∈N*),求数列{bn}的前n项和Tn.
(n∈N*),求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第五章 数列(解析版) 题型:选择题
数列{an}中,a1=1,对所有的n≥2,都有a1·a2·a3·…·an=n2,则a3+a5等于( )
A.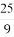 B.
B.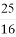 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第三章 三角函数、解三角形(解析版) 题型:解答题
(2014·孝感模拟)已知函数f(x)= sinωxcosωx-cos2ωx,其中ω为使f(x)能在x=
sinωxcosωx-cos2ωx,其中ω为使f(x)能在x= 时取得最大值的最小正整数.
时取得最大值的最小正整数.
(1)求ω的值.
(2)设△ABC的三边长a,b,c满足b2=ac,且边b所对的角θ的取值集合为M,当x∈M时,求f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com