
【题目】已知函数![]() (
(![]() 为常数).
为常数).
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)是否存在正实数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,若存在,求出实数
,若存在,求出实数![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(Ⅲ)当![]() 时,
时, ![]() ,对
,对![]() 恒成立,求整数
恒成立,求整数![]() 的最大值.
的最大值.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)2.
【解析】
(Ⅰ)由![]() ,讨论
,讨论![]() 和
和![]() 导数的正负,从而可得函数的单调性;
导数的正负,从而可得函数的单调性;
(Ⅱ)由正实数a,结合(Ⅰ)的单调性可得![]() ,即g(x)=f(x)+
,即g(x)=f(x)+![]() 在
在![]() 上单调递减,求导可得a
上单调递减,求导可得a![]() 对
对![]() 恒成立,分析不等式右边函数的最值即可;
恒成立,分析不等式右边函数的最值即可;
(Ⅲ)由题意得lnx![]() 对
对![]() 恒成立,当x=1时,b
恒成立,当x=1时,b![]() ; 又 b
; 又 b![]() ,通过证明b=2时不等式成立即可得解.
,通过证明b=2时不等式成立即可得解.
(Ⅰ)∵![]() ,
,![]() .
.
∴(ⅰ)若![]() ,则
,则![]() 恒成立
恒成立![]() f(x)在
f(x)在![]() 上单调递增;
上单调递增;
(ⅱ)若![]() ,则
,则![]() .
.
令![]() ,解得
,解得![]() ;令
;令![]() ,解得
,解得![]() .
.
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
综上:当![]() 时,f(x)在
时,f(x)在![]() 上单调递增;
上单调递增;
当![]() 时,f(x)在
时,f(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)满足条件的a不存在.理由如下:
若![]() ,由(Ⅰ)可知,函数f(x)=alnx+
,由(Ⅰ)可知,函数f(x)=alnx+![]() 在
在![]() 为增函数;
为增函数;
不妨设![]() ,
,
则![]() ,即
,即![]()
∴由题意:g(x)=f(x)+![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() 在
在![]() 上恒成立,即a
上恒成立,即a![]() 对
对![]() 恒成立;
恒成立;
又![]() 在
在![]() 上单调递减;
上单调递减;
∴a![]() ;故满足条件的正实数a不存在.
;故满足条件的正实数a不存在.
(Ⅲ)当a=1时,使![]() 对
对![]() 恒成立
恒成立
即lnx![]() 对
对![]() 恒成立.
恒成立.
∴ 当x=1时,b![]() ; 又 b
; 又 b![]()
下面证明:当b=2时,lnx![]() 对
对![]() 恒成立.
恒成立.
当b=2时,lnx![]() .
.
设g(x)=![]() ,则
,则![]() .
.
易知:![]()
![]() ,
,
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
∴g(x)![]()
即当b=2时,lnx![]() 对
对![]() 恒成立.∴
恒成立.∴![]()


科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
某产品按行业生产标准分成8个等级,等级系数X依次为1,2,……,8,其中X≥5为标准A,X≥3为标准B,已知甲厂执行标准A生产该产品,产品的零售价为6元/件;乙厂执行标准B生产该产品,产品的零售价为4元/件,假定甲、乙两厂得产品都符合相应的执行标准
(I)已知甲厂产品的等级系数X1的概率分布列如下所示:

且X1的数字期望EX1=6,求a,b的值;
(II)为分析乙厂产品的等级系数X2,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下:
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数X2的数学期望.
![]() 在(I)、(II)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.
在(I)、(II)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.
注:(1)产品的“性价比”=![]() ;
;
(2)“性价比”大的产品更具可购买性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,若函数
时,若函数![]() 与函数
与函数![]() 的图像总有两个交点,设两个交点的横坐标分别为
的图像总有两个交点,设两个交点的横坐标分别为![]() ,
,![]() .
.
①求![]() 的取值范围;
的取值范围;
②求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域是
的定义域是![]() ,有下列四个命题,其中正确的有( )
,有下列四个命题,其中正确的有( )
A.对于![]() (
(![]() ,0),函数
,0),函数![]() 在
在![]() 上是单调增函数
上是单调增函数
B.对于![]() (0,
(0,![]() ),函数
),函数![]() 存在最小值
存在最小值
C.存在![]() (
(![]() ,0),使得对于任意
,0),使得对于任意![]() ,都有
,都有![]() 成立
成立
D.存在![]() (0,
(0,![]() ),使得函数
),使得函数![]() 有两个零点
有两个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)设![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最小值;
上的最小值;
(3)某同学发现:总存在正实数![]() ,
,![]() ,使
,使![]() ,试问:该同学的判断是否正确?若不正确,请说明理由;若正确,请直接写出
,试问:该同学的判断是否正确?若不正确,请说明理由;若正确,请直接写出![]() 的取值范围(不需要解答过程).
的取值范围(不需要解答过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人的月工资由基础工资和绩效工资组成2010年每月的基础工资为2100元、绩效工资为2000元从2011年起每月基础工资比上一年增加210元、绩效工资为上一年的![]() 照此推算,此人2019年的年薪为______万元(结果精确到
照此推算,此人2019年的年薪为______万元(结果精确到![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从5名男生和4名女生中选出4人参加辩论比赛.
(1)如果男生中的甲与女生中的乙至少要有1人在内,那么有多少种不同选法?
(2)如果4个人中既有男生又有女生,那么有多少种不同选法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
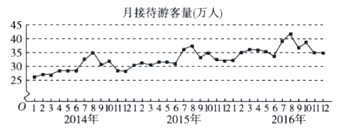
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com