
分析 (1)设椭圆标准方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),由已知得b=2$\sqrt{3}$,e=$\frac{c}{a}$=$\frac{1}{2}$,由此能求出椭圆C的标准方程.
(2)先求出|PQ|=6,设直线AB的方程为$y=\frac{1}{2}x+m$,与$\frac{x^2}{16}+\frac{y^2}{12}=1$联立,得x2+mx+m2-12=0,由此利用根的判别式、韦达定理、椭圆弦长公式,结合已知能求出四边形APBQ面积的最大值.
解答 解:(1)∵椭圆C的中心在原点,焦点在x轴上,
设椭圆标准方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0),
∵椭圆的离心率等于$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.
${x^2}=8\sqrt{3}y$焦点为$(0,2\sqrt{3})$…(1分)
∴b=2$\sqrt{3}$…(2分)e=$\frac{c}{a}$=$\frac{1}{2}$,a2+b2=c2,
∴解得a2=16,b2=12,
∴椭圆C的标准方程$\frac{x^2}{16}+\frac{y^2}{12}=1$.…(4分)
(2)直线 x=-2与椭圆$\frac{x^2}{16}+\frac{y^2}{12}=1$交点P(-2,-3),Q(-2,3)或P(-2,-3),Q(-2,3),
∴|PQ|=6,…(5分)
设A (x1,y1 ),B( x2,y2),直线AB的方程为 $y=\frac{1}{2}x+m$,
与$\frac{x^2}{16}+\frac{y^2}{12}=1$联立得x2+mx+m2-12=0…(6分)
由△=m2-4(m2-12)>0,得-4<m<4,…(7分)
由韦达定理得x1+x2=-m,${x_1}{x_2}={m^2}-12$,…(8分)
由A,B两点位于直线x=-2两侧,得(x1+2)(x2+2)<0,
即x1x2+2(x1+x2)+4<0,∴m2-2m-8<0,
解得-2<m<4,…(9分)
∴S=$\frac{1}{2}$•|PQ|•|x1-x2|
=$\frac{1}{2}$•|PQ|•$\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$
=3$\sqrt{48-3{m^2}}$,
∴当m=0时,S最大值为$12\sqrt{3}$.…(12分)
点评 本题考查椭圆标准方程的求法,考查四边形面积的最大值的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、椭圆弦长公式的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | f(1.5)<f(3.5)<f(6.5) | B. | f(6.5)<f(1.5)<f(3.5) | C. | f(6.5)<f(3.5)<f(1.5) | D. | f(3.5)<f(6.5)<f(1.5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 140石 | B. | 160石 | C. | 180石 | D. | 200石 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
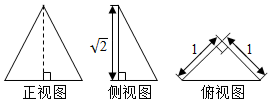
| A. | $\frac{32π}{3}$ | B. | 4π | C. | 2π | D. | $\frac{4π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com