解:(Ⅰ)F(x)=

-1+lnx.
F′(x)=
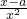
,
①当a≤0时,F′(x)≥0,
∴F(x)在(0,3)上是增函数;
②当0<a<3时,x∈(0,a)时,F′(x)≤0,∴F(x)在(0,a)上是减函数;
x∈(a,3)时,F′(x)≥0,∴F(x)在(a,3)上是增函数.
③当a≥3时,F′(x)≤0,∴F(x)在(0,3)上是减函数.…(4分)
(Ⅱ)令a=1,则F(x)=

-1+lnx,于是F′(x)=

,
∴F(x)在(0,1)上是减函数,在(1,+∞)上是增函数.
∴在区间(0,+∞)上F(x)有F(x)
min=F(1)=0.
∵
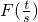
≥F(1)=0,
即
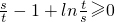
≥0,
整理得

≥
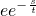
,即
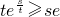
,即t
te
s≥s
te
t.…(8分)
(III)由已知得
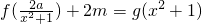
,代入整理得
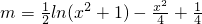
.
于是题意即为直线y=m与y=
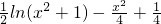
的图象有4个不同的交点.
令h(x)=
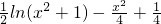
,
则
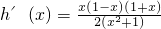
.
| x | (-∞,-1) | -1 | (-1,0) | 0 | (0,1) | 1 | (1,+∞) |
| h′(x) | + | 0 | - | 0 | + | 0 | - |
| h(x) | ↗ | 极大值
 | ↘ | 极小值 | ↗ | 极大值
 | ↘ |
可绘出h(x)的大致图象如图.

由图象可知当m∈(

,

)时满足有四个不同的交点.
∴存在实数
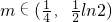
时满足条件.…(14分)
分析:(I)求出F(x)的导函数,通过对参数a的讨论,判断出导函数的符号,进一步得到函数的单调性.
(II)先求出当a=1时F(x)的导函数,通过导函数判断出函数的单调性,求出函数的最小值,得到
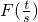
≥F(1)=0,整理不等式得到所要证的不等式.
(III)由已知得
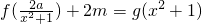
,分离出参数m,构造函数h(x),通过导数求出函数的单调性及极值,画出函数h(x)的草图,判断出m的范围.
点评:本题考查通过利用导数解决函数在闭区间上的最值问题,若含参数一般需要讨论;通过利用导数求函数的极值问题及单调性,进一步可画出函数的草图,解决两个函数的交点个数问题,属于难题.

 -1(其中a是不为0的实数),g(x)=lnx,设F(x)=f(x)+g(x).
-1(其中a是不为0的实数),g(x)=lnx,设F(x)=f(x)+g(x).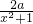 )+2m的图象与函数y=g(x2+1)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由.
)+2m的图象与函数y=g(x2+1)的图象恰好有四个不同的交点?若存在,求出m的取值范围,若不存在,说明理由. -1+lnx.
-1+lnx.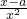 ,
, -1+lnx,于是F′(x)=
-1+lnx,于是F′(x)= ,
,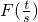 ≥F(1)=0,
≥F(1)=0,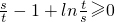 ≥0,
≥0, ≥
≥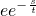 ,即
,即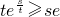 ,即ttes≥stet.…(8分)
,即ttes≥stet.…(8分)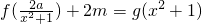 ,代入整理得
,代入整理得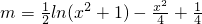 .
.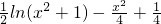 的图象有4个不同的交点.
的图象有4个不同的交点.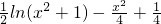 ,
,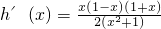 .
.


 由图象可知当m∈(
由图象可知当m∈( ,
, )时满足有四个不同的交点.
)时满足有四个不同的交点.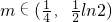 时满足条件.…(14分)
时满足条件.…(14分)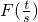 ≥F(1)=0,整理不等式得到所要证的不等式.
≥F(1)=0,整理不等式得到所要证的不等式.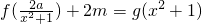 ,分离出参数m,构造函数h(x),通过导数求出函数的单调性及极值,画出函数h(x)的草图,判断出m的范围.
,分离出参数m,构造函数h(x),通过导数求出函数的单调性及极值,画出函数h(x)的草图,判断出m的范围.

 名校课堂系列答案
名校课堂系列答案