
| A. | 2016 | B. | 3024 | C. | 4032 | D. | 5040 |
分析 要求f=a${\;}_{1}^{3}$+a${\;}_{2}^{3}$+…+a${\;}_{2016}^{3}$的最大值,必须a1,a2,…,a2016中含有足够的2.讨论其中含有1008个2和672个2的情况,即可得到所求最大值.
解答 解:要求f=a${\;}_{1}^{3}$+a${\;}_{2}^{3}$+…+a${\;}_{2016}^{3}$的最大值,
必须a1,a2,…,a2016中含有足够的2.
由a1,a2,…,a2016∈[-2,2],且a1+a2+…+a2016=0,
若a1,a2,…,a2016中有1008个2,则另外1008个数均为-2,
则f=0不为最大值;
若a1,a2,…,a2016中有672个2,1344个-1,
满足条件,且使得f取得最大值,且为672×23-1344=4032.
故选:C.
点评 本题考查数列和的最值的求法,注意运用根据条件分析各个项的情况,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
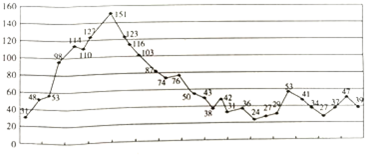
| 空气质量 指数类别 | 优 [0,35] | 良 (35,75] | 轻度污染 (75,115] | 中度污染 (115,150] | 重度污染 (150,250] | 严重污染 (250,500] | 合计 |
| 频数 | 30 | ||||||
| 频率 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
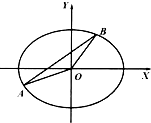 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
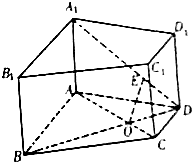 如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AB=4,AD=2$\sqrt{2}$,CD=2,AA1=2,侧棱AA1⊥底面ABCD,E是A1D上一点,且A1E=2ED.
如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AB=4,AD=2$\sqrt{2}$,CD=2,AA1=2,侧棱AA1⊥底面ABCD,E是A1D上一点,且A1E=2ED.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com