练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直线上取一点,过作以为焦点的椭圆，则当最小时，椭圆的标准方程为____________________.

    【答案】

    【解析】

    因为|MF1|+|MF2|=2a，即问题转化为在直线上求一点M，使M到F1，F2的距离的和最小，求出F1关于l的对称点F，即求M到F、F2的和最小，FF2的长就是所求的最小值．

    设F1（﹣3，0）关于l：x﹣y+9=0的对称点 F（x，y）

    则，即F（﹣9，6），

    连F2F交l于M，点M即为所求．

    F2F：即x+2y﹣3=0

    解方程组，即M（﹣5，4）

    当点M′取异于M的点时，|FM′|+|M′F2|＞|FF2|．

    满足题意的椭圆的长轴

    所以，b2=a2﹣c2=45﹣9=36

    所以椭圆的方程为：．

    故答案为：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知抛物线y＝x2－2x及直线x＝0，x＝a，y＝0围成的平面图形的面积为，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）= ，若互不相等的实数x1 ， x2 ， x3满足f（x1）=f（x2）=f（x3），则x1+x2+x3的取值范围是（ ）
    A.（ ]
    B.（ ）
    C.（ ]
    D.（ ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）在R上的导函数为f′（x），若f（x）＜2f′（x）恒成立，且f（ln4）=2，则不等式f（x）＞e 的解集是（ ）
    A.（ln2，+∞）
    B.（2ln2，+∞）
    C.（﹣∞，ln2）
    D.（﹣∞，2ln2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，已知圆x2+y2﹣12x+32=0的圆心为Q，过点P（0，2）且斜率为k的直线与圆Q相交于不同的两点A，B．
    （1）求k的取值范围；
    （2）是否存在常数k，使得向量 与 共线？如果存在，求k值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2cos（ωx﹣φ）（ω＞0，φ∈[0，π]）的部分图象如图所示，若A（ ， ），B（ ， ）．则下列说法错误的是（ ）

    A.φ=
    B.函数f（x）的一条对称轴为x=
    C.为了得到函数y=f（x）的图象，只需将函数y=2sin2x的图象向右平移 个单位
    D.函数f（x）的一个单调减区间为[ ， ]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：x2＋y2＝9，点A(－5，0)，直线l：x－2y＝0.

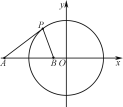
    (1)求与圆C相切，且与直线l垂直的直线方程；

    (2)在直线OA上(O为坐标原点)，存在定点B(不同于点A)，满足：对于圆C上任一点P，都有为一常数，试求所有满足条件的点B的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）= （x＞0），观察：
    f1（x）=f（x）= ，
    f2（x）=f（f1（x））= ；
    f3（x）=f（f2（x））= ．
    f4（x）=f（f3（x））=
    …
    根据以上事实，当n∈N*时，由归纳推理可得：fn（1）= ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在路边安装路灯,灯柱的高为米，路宽为23米，灯杆与灯柱角，路灯采用锥形灯罩，灯罩轴线与灯杆垂直，请你建立适当直角坐标系，解决以下问题:

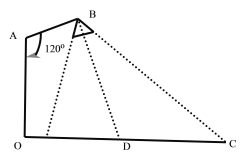
    (1)当

    （2）且灯罩轴线正好通过道路路面的中线时，求灯杆的长为多少米？

    查看答案和解析>>

    同步练习册答案