
 设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表的统计表格:
设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表的统计表格:| i | 1 | 2 | 3 | 4 | 5 | 合计 |
| xi(百万元) | 1.26 | 1.44 | 1.59 | 1.71 | 1.82 | 7.82 |
| wi(百万元) | 2.00 | 2.99 | 4.02 | 5.00 | 6.03 | 20.04 |
| yi(百万元) | 3.20 | 4.80 | 6.50 | 7.50 | 8.00 | 30.00 |
| $\overline{x}$=1.56,$\overline{w}$=4.01,$\overline{y}$=6,$\sum_{i=1}^{5}$xiyi=48.66,$\sum_{i=1}^{5}$wiyi=132.62,$\sum_{i=1}^{5}$(xi-$\overline{x}$)2=0.20,$\sum_{i=1}^{5}$(wi-$\overline{w}$)2=10.14 | ||||||
分析 (1)根据表中数据,绘制散点图,根据散点图可知,y=c+dx3适合作销售额y关于明星代言费x的回归方程;
(2)令ω=x3,则y=c+dω是y关于ω的线性回归方程,根据最小二乘法求得系数,求得回归方程,求得z的函数解析式,求导,利用z′≥0,求得z的单调递增区间,即可求得纯收益z随明星代言费z的增加而增加的区间.
解答 解:(1)散点图如图: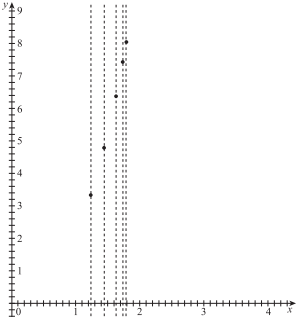
根据散点图可知,y=c+dx3适合作销售额y关于明星代言费x的回归方程.
(2)令ω=x3,则y=c+dω是y关于ω的线性回归方程,
所以$\widehat{d}$=$\frac{\sum_{i=1}^{5}{ω}_{i}•{y}_{i}-5\overline{ω}•\overline{y}}{\sum_{i=1}^{5}({ω}_{i}-\overline{ω})^{2}}$=1.21,$\widehat{c}$=$\overline{y}$-$\overline{d}$•$\overline{ω}$=1.15,
所以y=1.15+1.21ω=1.15+1.21x3.
z=0.2y-2.904x=0.2(1.15+1.21x3)-2.904x=0.242x3-2.904x+0.23,
令z'=0.726x2-2.904≥0,由x∈(0,300],解得:200≤x≤300.
估计:当明星代言费200≤x≤300百万元时,纯收益z随明星代言费x的增加而增加.
点评 本题考查独立性检验的应用,考查利用最小二乘法求回归直线方程,利用导数求函数单调性的方法,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 小明 | 6 | 6 | 9 | 9 |
| 小红 | 7 | 9 | 6 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 正方体ABCD-A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,点P在对角线BD1上,给出以下命题:
正方体ABCD-A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,点P在对角线BD1上,给出以下命题:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24种 | B. | 36种 | C. | 48种 | D. | 60种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 不很了解 | 了解 | 非常了解 | |
| 50岁以上 | 100 | 212 | y |
| 50岁以下 | x | 188 | z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com