Question

16．正方体ABCD-A₁B₁C₁D₁中，M，N，Q分别是棱D₁C₁，A₁D₁，BC的中点，点P在对角线BD₁上，给出以下命题：
①当P在BD₁上运动时，恒有MN∥面APC；
②若A，P，M三点共线，则$\frac{BP}{B{D}_{1}}$=$\frac{2}{3}$；
③若$\frac{BP}{B{D}_{1}}$=$\frac{2}{3}$，则C₁Q∥面APC；
④过点P且与直线AB₁和A₁C₁所成的角都为60°的直线有且只有3条．
其中正确命题的个数为（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 ①利用三角形中位线定理、正方体的性质可得MN∥AC，再利用线面平行的判定定理即可判断出正误；
②若A，P，M三点共线，由D₁M∥AB，由平行线的性质可得$\frac{{D}_{1}P}{BP}=\frac{{D}_{1}M}{AB}$=$\frac{1}{2}$，即可判断出正误；
③若$\frac{BP}{B{D}_{1}}$=$\frac{2}{3}$，由②可得：A，P，M三点共线，设对角线BD∩AC=O，可得四边形OQC₁M是平行四边形，于是C₁Q∥OM，即可判断出正误．
④连接B₁C，A₁C₁∥AC，由正方体的性质可得△AB₁C是等边三角形，则点P取点D₁，则直线AD₁，CD₁满足条件，有且只有这两条，即可判断出正误．

解答 解：如图所示，连接MN，AC，A₁C₁．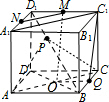
①当P在BD₁上运动时，M，N，分别是棱D₁C₁，A₁D₁的中点，由三角形中位线定理可得MN∥A₁C₁，由正方体的性质可得：A₁C₁∥AC．
∴MN∥AC，而MN?平面APC，AC?平面APC，∴恒有MN∥面APC，正确；
②若A，P，M三点共线，由D₁M∥AB，∴$\frac{{D}_{1}P}{BP}=\frac{{D}_{1}M}{AB}$=$\frac{1}{2}$，则$\frac{BP}{B{D}_{1}}$=$\frac{2}{3}$，正确；
③若$\frac{BP}{B{D}_{1}}$=$\frac{2}{3}$，由②可得：A，P，M三点共线，设对角线BD∩AC=O，连接OM，OQ，则四边形OQC₁M是平行四边形，∴C₁Q∥OM，而M点在平面APC内，∴C₁Q∥平面APC相交，因此正确；
④连接B₁C，A₁C₁∥AC，由正方体的性质可得△AB₁C是等边三角形，则点P取点D₁，则直线AD₁，CD₁满足条件，∴过点P且与直线AB₁和A₁C₁所成的角都为60°的直线有且只有2条，因此不正确．
综上可得：只有①②③正确，即正确的个数是3．
故选：C．

点评 本题考查了空间位置关系的判定、线面面面平行的判定与性质定理、等边三角形的性质、三角形中位线定理与平行四边形的性质、正方体的性质，考查了推理能力与计算能力，属于难题．