
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
分析 利用双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程为y=$\frac{1}{2}$x,可得a=2b,即可求出双曲线的离心率.
解答 解:∵双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程为y=$\frac{1}{2}$x,
∴a=2b,
∴c=$\sqrt{5}$b,
∴双曲线的离心率是e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$.
故选:A.
点评 本题考查双曲线的离心率的求法,是中档题,解题时要认真审题,要熟练掌握双曲线的简单性质.


科目:高中数学 来源: 题型:解答题
 设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表的统计表格:
设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表的统计表格:| i | 1 | 2 | 3 | 4 | 5 | 合计 |
| xi(百万元) | 1.26 | 1.44 | 1.59 | 1.71 | 1.82 | 7.82 |
| wi(百万元) | 2.00 | 2.99 | 4.02 | 5.00 | 6.03 | 20.04 |
| yi(百万元) | 3.20 | 4.80 | 6.50 | 7.50 | 8.00 | 30.00 |
| $\overline{x}$=1.56,$\overline{w}$=4.01,$\overline{y}$=6,$\sum_{i=1}^{5}$xiyi=48.66,$\sum_{i=1}^{5}$wiyi=132.62,$\sum_{i=1}^{5}$(xi-$\overline{x}$)2=0.20,$\sum_{i=1}^{5}$(wi-$\overline{w}$)2=10.14 | ||||||
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 过定点(0,1) | B. | 过定点(0,2) | C. | 过定点(a,1) | D. | 过定点(a,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | -2016 | C. | 2017 | D. | -2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | [-2,+∞) | C. | (-3,+∞) | D. | (-$\frac{9}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
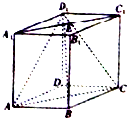 已知四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形.
已知四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD,底面ABCD为菱形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com