
���� ��1����֪b1=S1+2=4����Sn+1=2Sn+2�ɵ�bn+1=2bn���Ӷ�֤����
��2���ɣ�1��֪Sn=2n+1-2���Ӷ����������е�ͨ�ʽ��
��3������cn=n-��$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+��+$\frac{1}{{2}^{n}}$��=n-1+$\frac{1}{{2}^{n}}$���Ӷ���������ͣ�
��� �⣺��1��֤����b1=S1+2=4��
��Sn+1=2Sn+2����Sn+1+2=2Sn+4=2��Sn+2����
��bn+1=2bn��
������{bn}����4Ϊ���2Ϊ���ȵĵȱ����У�
��2���ɣ�1��֪��bn=Sn+2=4•2n-1=2n+1��
��Sn=2n+1-2��
��n=1ʱ��a1=S1=2��
��n��2ʱ��an=Sn-Sn-1=��2n+1-2��-��2n-2��=2n��
��n=1ʱ��ʽҲ������
��an=2n��
��3��cn=$\frac{{a}_{1}-1}{2}$+$\frac{{a}_{2}-1}{{2}^{2}}$+��+$\frac{{a}_{n}-1}{{2}^{n}}$=$\frac{2-1}{2}$+$\frac{{2}^{2}-1}{{2}^{2}}$+��+$\frac{{2}^{n}-1}{{2}^{n}}$
=n-��$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+��+$\frac{1}{{2}^{n}}$��=n-1+$\frac{1}{{2}^{n}}$��
��Tn=0+$\frac{1}{2}$+��1+$\frac{1}{{2}^{2}}$��+��+��n-1+$\frac{1}{{2}^{n}}$��
=$\frac{0+n-1}{2}$•n+1-$\frac{1}{{2}^{n}}$
=$\frac{1}{2}$n��n-1��+1-$\frac{1}{{2}^{n}}$��
���� ���⿼�������е����ʵ��ж���Ӧ�ã�ͬʱ�����˷������۵�˼��Ӧ�ü������Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{2}$ | B�� | $\frac{15}{2}$ | C�� | $\frac{15}{7}$ | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
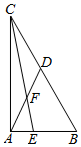 ��֪$\overrightarrow{AB}$��$\overrightarrow{AC}$��|$\overrightarrow{AB}-\overrightarrow{AC}$|=2��D�DZ�BC���е㣬$\overrightarrow{AE}$=$\frac{1}{3}\overrightarrow{AB}$
��֪$\overrightarrow{AB}$��$\overrightarrow{AC}$��|$\overrightarrow{AB}-\overrightarrow{AC}$|=2��D�DZ�BC���е㣬$\overrightarrow{AE}$=$\frac{1}{3}\overrightarrow{AB}$�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
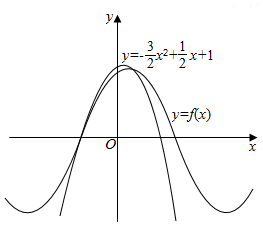 ��ͼ��ʾ������f��x��=sin����x+�գ����أ�0��|��|��$\frac{��}{2}$����y���������������ֵ����������y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1�ϣ���f��x��=sin��$\frac{��}{2}$x+$\frac{��}{3}$����
��ͼ��ʾ������f��x��=sin����x+�գ����أ�0��|��|��$\frac{��}{2}$����y���������������ֵ����������y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1�ϣ���f��x��=sin��$\frac{��}{2}$x+$\frac{��}{3}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{56}{65}$ | B�� | $\frac{33}{65}$ | C�� | $\frac{5}{6}$ | D�� | $\frac{16}{65}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | ����ֲ���Ҫ���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com