
(本小题满分14分)
已知函数 在
在 上有定义,对任意实数
上有定义,对任意实数 和任意实数
和任意实数 ,都有
,都有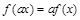 .
.
(Ⅰ)证明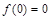 ;
;
(Ⅱ)证明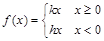 (其中k和h均为常数);
(其中k和h均为常数);
(Ⅲ)当(Ⅱ)中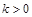 的时,设
的时,设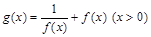 ,讨论
,讨论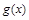 在
在 内的单调性.
内的单调性.
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:解答题
(本题满分14分)
某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1000辆.本年度为适应市场需求,计划提高产品档次,适度增加投入成本.若每辆车投入成本增加的比例为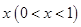 ,则出厂价相应提高的比例为
,则出厂价相应提高的比例为 ,同时预计年销售量增加的比例为
,同时预计年销售量增加的比例为 .已知年利润=(出厂价–投入成本)
.已知年利润=(出厂价–投入成本)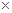 年销售量.
年销售量.
(1)写出本年度预计的年利润 与投入成本增加的比例
与投入成本增加的比例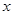 的关系式;
的关系式;
(2)为使本年度的年利润比上年有所增加,问投入成本增加的比例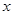 应在什么范围内?
应在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知26辆货车以相同速度v由A地驶向400千米处的B地,每两辆货车间距离为d千米,现已知d与v的平方成正比,且当v=20(千米/时)时,d=1(千米).
(1)写出d与v的函数关系;
(2)若不计货车的长度,则26辆货车都到达B地最少需要多少小时?此时货车速度是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂需要围建一个面积为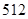 平方米的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁,问堆料场的长和宽各为多少时,才能使砌墙所用的材料最省?
平方米的矩形堆料场,一边可以利用原有的墙壁,其他三边需要砌新的墙壁,问堆料场的长和宽各为多少时,才能使砌墙所用的材料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;(2)若f(x)在区间[2a,a+1]上不单调,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com