练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f1(x)＝sin x＋cos x，记f2(x)＝f1′(x)，f3(x)＝f2′(x)，…，fn(x)＝fn－1′(x)(n∈N*，n≥2)，则f1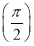＋f2＋…＋f2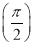 014＝________.

     

    0

    【解析】f2(x)＝f1′(x)＝cos x－sin x，

    f3(x)＝(cos x－sin x)′＝－sin x－cos x，

    f4(x)＝－cos x＋sin x，f5(x)＝sin x＋cos x，

    以此类推，可得出fn(x)＝fn＋4(x)，

    又∵f1(x)＋f2(x)＋f3(x)＋f4(x)＝0，

    ∴f1＋f2＋…＋f2 014

    ＝503f1＋f2＋f3＋f4＋f1＋f2＝0.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

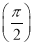    科目：高中数学 来源：2015届高考苏教数学（理）训练2 命题及其关系、充分条件与必要条件（解析版） 题型：填空题

    下列命题：

    ①若ac2>bc2，则a>b；

    ②若sin α＝sin β，则α＝β；

    ③“实数a＝0”是“直线x－2ay＝1和直线2x－2ay＝1平行”的充要条件；

    ④若f(x)＝log2x，则f(|x|)是偶函数．

    其中正确命题的序号是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届高考苏教数学（理）训练16 导数与函数的综合问题（解析版） 题型：填空题

    函数f(x)＝ax3＋x恰有三个单调区间，则a的取值范围是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届高考苏教数学（理）训练15 导数与函数极值、最值（解析版） 题型：填空题

    当函数y＝x·2x取极小值时，x＝________.

     

    查看答案和解析>>

    科目：高中数学 来源：2015届高考苏教数学（理）训练14 导数与函数单调性（解析版） 题型：填空题

    若函数f(x)＝x2＋ax＋在上是增函数，则a的取值范围是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届高考苏教数学（理）训练13 变化率与导数、导数的计算（解析版） 题型：填空题

    已知点A(1,1)和B(－1，－3)在曲线C：y＝ax3＋bx2＋d(a，b，d均为常数)上．若曲线C在点A，B处的切线互相平行，则a3＋b2＋d＝________.

     

    查看答案和解析>>

    科目：高中数学 来源：2015届高考苏教数学（理）训练11 函数与方程（解析版） 题型：填空题

    已知0<a<1，k≠0，函数f(x)＝，若函数g(x)＝f(x)－k有两个零点，则实数k的取值范围是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届高考苏教数学（理）训练10 对数与对数函数（解析版） 题型：填空题

    函数y＝的定义域为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届高考数学（理）一轮总复习专题突破六 高考概率与统计（解析版） 题型：解答题

    某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物．根据历年的种植经验，一株该种作物的年收获量Y(单位：kg)与它的“相近”作物株数X之间的关系如下表所示：

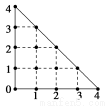
    X

    1

    2

    3

    4

    Y

    51

    48

    45

    42

     

    这里，两株作物“相近”是指它们之间的直线距离不超过1米．

    (1)从三角形地块的内部和边界上分别随机选取一株作物，求它们恰好“相近”的概率；

    (2)从所种作物中随机选取一株，求它的年收获量的分布列与数学期望．

     

    查看答案和解析>>

    同步练习册答案