练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知点A(1,1)和B(－1，－3)在曲线C：y＝ax3＋bx2＋d(a，b，d均为常数)上．若曲线C在点A，B处的切线互相平行，则a3＋b2＋d＝________.

     

    7

    【解析】由题意得y′＝3ax2＋2bx，因为k1＝k2，所以3a＋2b＝3a－2b，即b＝0.又a＋d＝1，d－a＝－3，所以d＝－1，a＝2，即a3＋b2＋d＝7.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015届高考苏教数学（理）训练2 命题及其关系、充分条件与必要条件（解析版） 题型：填空题

    下列命题中为真命题的是________．(填写序号)

    ①命题“若x>y，则x>|y|”的逆命题

    ②命题“x>1，则x2>1”的否命题

    ③命题“若x＝1，则x2＋x－2＝0”的否命题

    ④命题“若x2>0，则x>1”的逆否命题

     

    查看答案和解析>>

    科目：高中数学 来源：2015届高考苏教数学（理）训练15 导数与函数极值、最值（解析版） 题型：解答题

    已知函数f(x)＝(x－a)(x－b)2，a，b是常数．

    (1)若a≠b，求证：函数f(x)存在极大值和极小值；

    (2)设(1)中f(x)取得极大值、极小值时自变量的值分别为x1，x2，设点A(x1，f(x1))，B(x2，f(x2))．如果直线AB的斜率为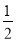－，求函数f(x)和f′(x)的公共递减区间的长度；

    (3)若f(x)≥mxf′(x)对于一切x∈R恒成立，求实数m，a，b满足的条件．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届高考苏教数学（理）训练14 导数与函数单调性（解析版） 题型：解答题

    已知函数f(x)＝ln x＋2x，g(x)＝a(x2＋x)．

    (1)若a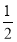＝，求F(x)＝f(x)－g(x)的单调区间；

    (2)若f(x)≤g(x)恒成立，求实数a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届高考苏教数学（理）训练13 变化率与导数、导数的计算（解析版） 题型：填空题

    已知f1(x)＝sin x＋cos x，记f2(x)＝f1′(x)，f3(x)＝f2′(x)，…，fn(x)＝fn－1′(x)(n∈N*，n≥2)，则f1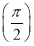＋f2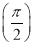＋…＋f2 014＝________.

     

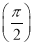    查看答案和解析>>

    科目：高中数学 来源：2015届高考苏教数学（理）训练11 函数与方程（解析版） 题型：解答题

    关于x的二次方程x2＋(m－1)x＋1＝0在区间[0,2]上有解，求实数m的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届高考苏教数学（理）训练11 函数与方程（解析版） 题型：填空题

    已知函数y＝f(x)的图像是连续不间断的曲线，且有如下的对应值：

    x

    1

    2

    3

    4

    5

    6

    y

    124.4

    35

    －74

    14.5

    －56.7

    －123.6

     

    则函数y＝f(x)在区间[1,6]上的零点至少有________个．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届高考苏教数学（理）训练1 集合（解析版） 题型：填空题

    已知集合A＝{x|x2－2x＋a>0}，且1∉A，则实数a的取值范围是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015届高考数学（理）一轮总复习专题突破六 高考概率与统计（解析版） 题型：填空题

    某工厂经过技术改造后，降低了能源消耗，经统计该厂某种产品的产量x(单位：吨)与相应的生产能耗y(单位：吨)有如下几组样本数据：

    x

    3

    4

    5

    6

    y

    2.5

    3

    4

    4.5

    根据相关性检验，这组样本数据具有线性相关关系，通过线性回归分析，求得回归直线的斜率为0.7.已知该产品的年产量为10吨，则该工厂每年大约消耗的汽油为________吨．

     

    查看答案和解析>>

    同步练习册答案