
已知函数f(x)=(x-a)(x-b)2,a,b是常数.
(1)若a≠b,求证:函数f(x)存在极大值和极小值;
(2)设(1)中f(x)取得极大值、极小值时自变量的值分别为x1,x2,设点A(x1,f(x1)),B(x2,f(x2)).如果直线AB的斜率为-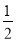 ,求函数f(x)和f′(x)的公共递减区间的长度;
,求函数f(x)和f′(x)的公共递减区间的长度;
(3)若f(x)≥mxf′(x)对于一切x∈R恒成立,求实数m,a,b满足的条件.
(1)见解析 (2)公共减区间为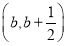 或
或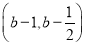 ,长度均为
,长度均为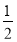
(3)m=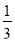 ,a=b≤0.
,a=b≤0.
【解析】【解析】
(1)证明:
f′(x)=(x-b)[3x-(2a+b)],
因为a≠b,所以b≠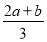 ,
,
所以f′(x)=0有两个不等实根b和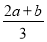 ,
,
所以f(x)存在极大值和极小值.
(2)①当a=b时,f(x)不存在减区间;
②当a>b时,由(1)知x1=b,x2=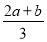 ,
,
所以A(b,0),B ,
,
所以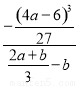 =-
=-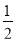 ,
,
即4(a-b)3=9(a-b),
所以a-b=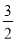 或a-b=-
或a-b=-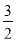 (舍去);
(舍去);
③当a<b时,x1=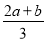 ,x2=b.
,x2=b.
同理可得a-b=-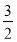 或a-b=
或a-b=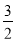 (舍去).
(舍去).
综上,a>b且a-b=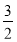 或a<b且a-b=-
或a<b且a-b=- .
.
所以f(x)的减区间为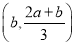 ,即(b,b+1)或f(x)的减区间为
,即(b,b+1)或f(x)的减区间为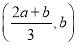 ,即(b-1,b);
,即(b-1,b);
f′(x)的减区间为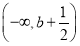 或
或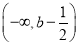 .
.
所以公共减区间为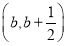 或
或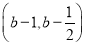 ,长度均为
,长度均为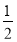 .
.
(3)由题意f(x)≥mxf′(x),
所以(x-a)(x-b)2≥mx(x-b)[3x-(2a+b)],
所以(x-b){(1-3m)x2+[m(2a+b)-(a+b)]x+ab}≥0.
若m≠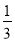 ,则左边是一个一次因式乘一个恒正(或恒负)的二次三项式,或者是三个一次因式的积,无论哪种情况,总有一个一次因式的指数是奇次的,这个因式的零点左右的符号不同,因此不可能恒非负.
,则左边是一个一次因式乘一个恒正(或恒负)的二次三项式,或者是三个一次因式的积,无论哪种情况,总有一个一次因式的指数是奇次的,这个因式的零点左右的符号不同,因此不可能恒非负.
所以m=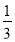 ,
,
所以(x-b)[(a+2b)x-3ab]≤0.
若a+2b=0,则a=-2b,所以a=b=0;
若a+2b≠0,则x1=b,x2=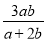 ,
,
所以
①若b=0,则a<0;
②若b≠0,则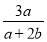 =1,所以a=b且b<0.
=1,所以a=b且b<0.
综上,m=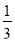 ,a=b≤0.
,a=b≤0.


科目:高中数学 来源:2015届高考苏教数学(理)训练5 函数的单调性与最值(解析版) 题型:填空题
设函数f(x)=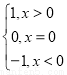 ,g(x)=x2f(x-1),则函数g(x)的递减区间是________.
,g(x)=x2f(x-1),则函数g(x)的递减区间是________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练18 同角三角函数的基本关系与诱导公式(解析版) 题型:填空题
已知sin(π-α)=log8 ,且α∈
,且α∈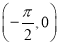 ,则tan(2π-α)的值为________.
,则tan(2π-α)的值为________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练17 任意角和弧度制及任意角的三角函数(解析版) 题型:填空题
将表的分针拨快10分钟,则分针旋转过程中形成的角的弧度数是______.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练16 导数与函数的综合问题(解析版) 题型:填空题
函数f(x)=ax3+x恰有三个单调区间,则a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:填空题
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0; ②f(0)f(1)<0;
③f(0)f(3)>0; ④f(0)f(3)<0.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练13 变化率与导数、导数的计算(解析版) 题型:填空题
已知点A(1,1)和B(-1,-3)在曲线C:y=ax3+bx2+d(a,b,d均为常数)上.若曲线C在点A,B处的切线互相平行,则a3+b2+d=________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学训练3 简单的逻辑联结词、全称量词与存在量词(解析版) 题型:填空题
下列结论:
①若命题p:?x0∈R,tan x0=2;命题q:?x∈R,x2-x+ >0.则命题“p∧(
>0.则命题“p∧( q)”是假命题;
q)”是假命题;
②已知直线l1:ax+3y-1=0,l2:x+by+1=0,则l1⊥l2的充要条件是 =-3;
=-3;
③“设a、b∈R,若ab≥2,则a2+b2>4”的否命题为:“设a、b∈R,若ab<2,则a2+b2≤4”.
其中正确结论的序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com