
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0; ②f(0)f(1)<0;
③f(0)f(3)>0; ④f(0)f(3)<0.
其中正确结论的序号是________.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源:2015届高考苏教数学(理)训练5 函数的单调性与最值(解析版) 题型:填空题
若函数f(x)=4x2-mx+5在[-2,+∞)上递增,在(-∞,-2]上递减,则f(1)=________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练16 导数与函数的综合问题(解析版) 题型:解答题
已知函数f(x)=ax+x2-xln a(a>0,a≠1).
(1)求函数f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)的单调增区间;
(3)若存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1(e是自然对数的底数),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:解答题
已知函数f(x)=(x-a)(x-b)2,a,b是常数.
(1)若a≠b,求证:函数f(x)存在极大值和极小值;
(2)设(1)中f(x)取得极大值、极小值时自变量的值分别为x1,x2,设点A(x1,f(x1)),B(x2,f(x2)).如果直线AB的斜率为-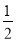 ,求函数f(x)和f′(x)的公共递减区间的长度;
,求函数f(x)和f′(x)的公共递减区间的长度;
(3)若f(x)≥mxf′(x)对于一切x∈R恒成立,求实数m,a,b满足的条件.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:填空题
定义在[1,+∞)上的函数f(x)满足:①f(2x)=cf(x)(c为正常数);②当2≤x≤4时,f(x)=1-|x-3|.若函数的所有极大值点均落在同一条直线上,则c=________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练14 导数与函数单调性(解析版) 题型:解答题
已知函数f(x)=ln x+2x,g(x)=a(x2+x).
(1)若a=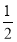 ,求F(x)=f(x)-g(x)的单调区间;
,求F(x)=f(x)-g(x)的单调区间;
(2)若f(x)≤g(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练11 函数与方程(解析版) 题型:解答题
关于x的二次方程x2+(m-1)x+1=0在区间[0,2]上有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学训练3 简单的逻辑联结词、全称量词与存在量词(解析版) 题型:填空题
下列命题:
①命题“若x2-3x+2=0,则x=1”的否命题是“若x2-3x+2=0,则x≠1”;
②命题p:?x0∈R,sin x0>1,则 p:?x∈R,sin x≤1;
p:?x∈R,sin x≤1;
③若p且q为假命题,则p,q均为假命题;
④“φ=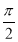 +2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件.
+2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件.
其中为真命题的是________(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com