
已知函数f(x)=ln x+2x,g(x)=a(x2+x).
(1)若a=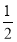 ,求F(x)=f(x)-g(x)的单调区间;
,求F(x)=f(x)-g(x)的单调区间;
(2)若f(x)≤g(x)恒成立,求实数a的取值范围.
(1)即函数F(x)的单调递增区间为(0,2),单调递减区间为(2,+∞).
(2)[1,+∞)
【解析】【解析】
(1)若a=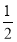 ,
,
则F(x)=ln x+2x-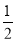 x2-
x2-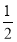 x,
x,
其定义域是(0,+∞),
则F′(x)=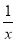 +2-x-
+2-x-
=-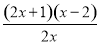 .
.
令F′(x)=0,得x=2,x=-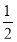 (舍去).
(舍去).
当0<x<2时,F′(x)>0,函数单调递增;
当x>2时,F′(x)<0,函数单调递减.
即函数F(x)的单调递增区间为(0,2),单调递减区间为(2,+∞).
(2)设F(x)=f(x)-g(x)
=ln x+2x-ax2-ax,
则F′(x)=-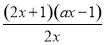 ,
,
当a≤0时,F′(x)≥0,F(x)单调递增,
F(x)≤0不可能恒成立;
当a>0时,令F′(x)=0,
得x=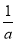 ,x=-
,x=-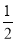 (舍去).
(舍去).
当0<x<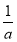 时,F′(x)>0,函数单调递增;
时,F′(x)>0,函数单调递增;
当x> 时,F′(x)<0,函数单调递减.
时,F′(x)<0,函数单调递减.
故F(x)在(0,+∞)上的最大值是F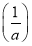 ,依题意F
,依题意F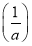 ≤0恒成立,
≤0恒成立,
即ln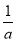 +
+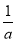 -1≤0.
-1≤0.
令g(a)=ln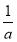 +
+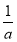 -1,又g(x)单调递减,且g(1)=0,故ln
-1,又g(x)单调递减,且g(1)=0,故ln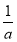 +
+ -1≤0成立的充要条件是a≥1,
-1≤0成立的充要条件是a≥1,
所以实数a的取值范围是[1,+∞).


科目:高中数学 来源:2015届高考苏教数学(理)训练17 任意角和弧度制及任意角的三角函数(解析版) 题型:填空题
将表的分针拨快10分钟,则分针旋转过程中形成的角的弧度数是______.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练15 导数与函数极值、最值(解析版) 题型:填空题
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.现给出如下结论:
①f(0)f(1)>0; ②f(0)f(1)<0;
③f(0)f(3)>0; ④f(0)f(3)<0.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练13 变化率与导数、导数的计算(解析版) 题型:填空题
已知点A(1,1)和B(-1,-3)在曲线C:y=ax3+bx2+d(a,b,d均为常数)上.若曲线C在点A,B处的切线互相平行,则a3+b2+d=________.
查看答案和解析>>
科目:高中数学 来源:2015届高考苏教数学(理)训练10 对数与对数函数(解析版) 题型:解答题
设f(x)=loga(1+x)+loga(3-x)(a>0,a≠1),且f(1)=2.
(1)求a的值及f(x)的定义域.
(2)求f(x)在区间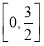 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破四 高考立体几何(解析版) 题型:填空题
如图,在三棱锥D-ABC中,若AB=BC,AD=CD,E是AC的中点,则平面ADC与平面BDE的关系是________.
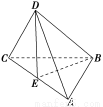
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com