
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{3π}{4}$ |
分析 求得向量$\overrightarrow{a}$的模,由向量垂直的条件:数量积为0,化简,再由数量积的定义和向量的平方即为模的平方,解方程可得向量夹角的余弦值,进而得到向量的夹角.
解答 解:向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$=(1,-1),|$\overrightarrow{b}$|=1,且$\overrightarrow{b}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$),
可得|$\overrightarrow{a}$|=$\sqrt{2}$,$\overrightarrow{b}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=0,
即为$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=0,
即有|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos<$\overrightarrow{a}$,$\overrightarrow{b}$>+|$\overrightarrow{b}$|2=$\sqrt{2}$cos<$\overrightarrow{a}$,$\overrightarrow{b}$>+1=0,
则cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=-$\frac{\sqrt{2}}{2}$,
由0≤<$\overrightarrow{a}$,$\overrightarrow{b}$>≤π,
可得$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{3π}{4}$.
故选:D.
点评 本题考查向量数量积的定义和向量垂直的条件:数量积为0,以及向量的平方即为模的平方,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2n | B. | 2n | C. | n2 | D. | nn |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x0∈R,sinx0>1”的否定是“?x∈R,sinx>1” | |
| B. | “若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0” | |
| C. | 在△ABC中,A>B是sinA>sinB的充分不必要条件 | |
| D. | 若p∧(¬q)为假,p∨(¬q)为真,则p,q同真或同假 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
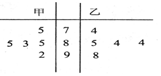 如图是某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)的茎叶图,甲、乙两位同学得分的中位数分别为x1,x2,得分的方差分别为y1,y2,则下列结论正确的是( )
如图是某班甲、乙两位同学在5次阶段性检测中的数学成绩(百分制)的茎叶图,甲、乙两位同学得分的中位数分别为x1,x2,得分的方差分别为y1,y2,则下列结论正确的是( )| A. | x1<x2,y1<y2 | B. | x1<x2,y1>y2 | C. | x1>x2,y1>y2 | D. | x1>x2,y1<y2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 工作日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| 限行车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1+x2≥$\frac{\sqrt{5}-1}{2}$ | B. | x1+x2<$\frac{\sqrt{5}-1}{2}$ | C. | x1+x2≥$\frac{\sqrt{5}+1}{2}$ | D. | x1+x2<$\frac{\sqrt{5}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\sqrt{3}$-1] | B. | (-∞,0] | C. | [0,$\sqrt{3}$-1] | D. | (-∞,1-$\sqrt{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com