
【题目】学校从参加高一年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为150分),数学成绩分组及各组频数如下:
[60,75),2;[75,90),3;[90,105),14;[105,120),15;[120,135),12;[135,150],4.
(1)在给出的样本频率分布表中,求A,B,C,D的值;
(2)估计成绩在120分以上(含120分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[135,150]的学生中选两位同学,共同帮助成绩在[60,75)中的某一位同学.已知甲同学的成绩为62分,乙同学的成绩为140分,求甲、乙两同学恰好被安排在同一小组的概率.
样本频率分布表:
分组 | 频数 | 频率 |
[60,75) | 2 | 0.04 |
[75,90) | 3 | 0.06 |
[90,105) | 14 | 0.28 |
[105,120) | 15 | 0.30 |
[120,135) | A | B |
[135,150] | 4 | 0.08 |
合计 | C | D |
【答案】
(1)解:由样本频率分布表,得:
C=50,A=50﹣2﹣3﹣14﹣15﹣4=12,B= ![]() =0.24,D=1
=0.24,D=1
(2)解:估计成绩在120分以上(含120分)的学生比例为:0.24+0.08=0.32
(3)成绩在[60,75)内有2人,记为甲、A,
成绩在[135,150]内有4人,记为乙,B,C,D,
则“二帮一”小组有以下12种分组办法:
甲乙B,甲乙C,甲乙D,甲BC,甲BD,甲CD,A乙B,A乙C,A乙D,ABC,ABD,ACD,
其中甲、乙两同学被分在同一小组有3种办法:甲乙B,甲乙C,甲乙D,
∴甲、乙同学恰好被安排在同一小组的概率为:p= ![]()
【解析】(1)由样本频率分布表,能求出A,B,C,D的值.(2)由频率分布表能估计成绩在120分以上(含120分)的学生比例.(3)成绩在[60,75)内有2人,记为甲、A,成绩在[135,150]内有4人,记为乙,B,C,D,由此利用列举法能求出甲、乙同学恰好被安排在同一小组的概率.
【考点精析】利用频率分布直方图对题目进行判断即可得到答案,需要熟知频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() )与直线
)与直线![]() :
: ![]() (
(![]() ),四点
),四点![]() ,
, ![]() ,
, ![]() ,
, ![]() 中有三个点在椭圆
中有三个点在椭圆![]() 上,剩余一个点在直线
上,剩余一个点在直线![]() 上.
上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若动点![]() 在直线
在直线![]() 上,过
上,过![]() 作直线交椭圆
作直线交椭圆![]() 于
于![]() ,
, ![]() 两点,使得
两点,使得![]() ,再过
,再过![]() 作直线
作直线![]() ,证明:直线
,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组,第一组[155,160),第二组[160,165),…,第八组[190.195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组人数为4. 
(1)求第七组的频数.
(2)估计该校的800名男生身高的中位数在上述八组中的哪一组以及身高在180cm以上(含180cm)的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
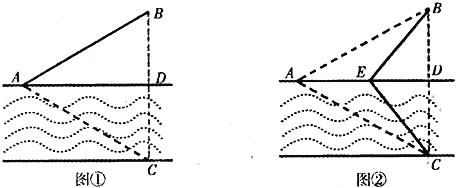
【题目】如图①,一条宽为1km的两平行河岸有村庄A和供电站C,村庄B与A、C的直线距离都是2km,BC与河岸垂直,垂足为D.现要修建电缆,从供电站C向村庄A、B供电.修建地下电缆、水下电缆的费用分别是2万元/km、4万元/km.
(1)已知村庄A与B原来铺设有旧电缆,但旧电缆需要改造,改造费用是0.5万元/km.现决定利用此段旧电缆修建供电线路,并要求水下电缆长度最短,试求该方案总施工费用的最小值;
(2)如图②,点E在线段AD上,且铺设电缆的线路为CE、EA、EB.若∠DCE=θ(0≤θ≤![]() ),试用θ表示出总施工费用y (万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y (万元)的解析式,并求y的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名同学8次数学测验成绩如茎叶图所示, ![]() 1 ,
1 , ![]() 2分别表示甲、乙两名同学8次数学测验成绩的平均数,s1 , s2分别表示甲、乙两名同学8次数学测验成绩的标准差,则有( )
2分别表示甲、乙两名同学8次数学测验成绩的平均数,s1 , s2分别表示甲、乙两名同学8次数学测验成绩的标准差,则有( )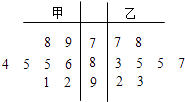
A.![]() 1>
1> ![]() 2 , s1<s2
2 , s1<s2![]()
B.![]() 1=
1= ![]() 2 , s1<s2
2 , s1<s2![]()
C.![]() 1=
1= ![]() 2 , s1=s2
2 , s1=s2 ![]()
D.![]() 1<
1< ![]() 2 , s1>s2
2 , s1>s2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com