
分析 (1)设圆C的圆心为C(a,b),根据圆C与圆x2+y2=0关于直线x+y+2=0对称,得到$\left\{\begin{array}{l}{\frac{a}{2}+\frac{b}{2}+2=0}\\{\frac{b}{a}=1}\end{array}\right.$,解得即可.
(2)过点P分别作圆O,圆C的两条切线PA,PB分别为A,B,有PA=PB,则点P一在OC的垂直平分线上,即在x+y+2=0上,点P也在直线l:2x+y-3=0上,即点P是直线l与直线x+y+2=0的交点,联立方程组,解得即可.
解答  解:(1)∵圆C与圆x2+y2=1关于直线x+y+2=0对称,
解:(1)∵圆C与圆x2+y2=1关于直线x+y+2=0对称,
∴圆C的半径r=1,
圆x2+y2=1的圆心(0,0),
设圆C的圆心为C(a,b),
∵圆C与圆x2+y2=0关于直线x+y+2=0对称,
∴$\left\{\begin{array}{l}{\frac{a}{2}+\frac{b}{2}+2=0}\\{\frac{b}{a}=1}\end{array}\right.$,
解得a=-2,b=-2.
∴圆的方程为(x+2)2+(y+2)2=1.
(2)过点P分别作圆O,圆C的两条切线PA,PB分别为A,B,有PA=PB,
∴点P一在OC的垂直平分线上,即在x+y+2=0上,
∵点P也在直线l:2x+y-3=0上,
∴点P是直线l与直线x+y+2=0的交点,
由$\left\{\begin{array}{l}{x+y+2=0}\\{2x+y-3=0}\end{array}\right.$,
解得x=5,y=-7,
∴P(5,-7)
点评 本题考查圆的方程的求法,公切线的性质,解题时要认真审题,注意圆的性质的合理运用.是中档题


科目:高中数学 来源: 题型:填空题
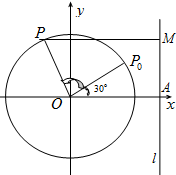 如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离|OA|=3,P0为圆周上一点,且∠AOP0=$\frac{π}{6}$,点P从P0处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动.t秒钟后,点P到直线l的距离用t(t≥0)可以表示为3-2cos(πt+$\frac{π}{6}$),t≥0.
如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离|OA|=3,P0为圆周上一点,且∠AOP0=$\frac{π}{6}$,点P从P0处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动.t秒钟后,点P到直线l的距离用t(t≥0)可以表示为3-2cos(πt+$\frac{π}{6}$),t≥0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
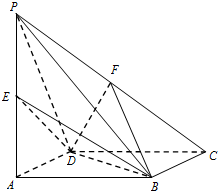 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[5-2\sqrt{2},5+2\sqrt{2}]$ | B. | $[\sqrt{5},\sqrt{29}]$ | C. | $[\sqrt{5},\sqrt{61}]$ | D. | $[\sqrt{29},\sqrt{61}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别 是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别 是PC,PD,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com