
分析 (1)把点(an,an+1)代入函数解析式,两边取对数,变形可得数列{lg(2an+1)}是以2为公比的等比数列;
(2)由(1)求出数列{an}的通项公式,证明$\frac{1}{a_n}$+$\frac{1}{{{a_n}+1}}$=$\frac{2}{{a}_{n}}$-$\frac{2}{{a}_{n+1}}$得答案;
(3)由(2)的结论,裂项相消求得Tn.
解答 (1)证明:由点(an,an+1)在函数f(x)=2x2+2x的图象上,得an+1=2${{a}_{n}}^{2}$+2an,
∴2an+1+1=2(2${{a}_{n}}^{2}$+2an)+1=$(2{a}_{n}+1)^{2}$,
两边取对数,得lg(2an+1+1)=2lg(2an+1),
∴数列{lg(2an+1)}是以2为公比的等比数列;
(2)证明:由(1)得:数列{lg(2an+1)}是以2为公比的等比数列,且lg(2a1+1)=lg5,
∴lg(2an+1)=2n-1•lg5,则2an+1=${5}^{{2}^{n-1}}$,∴${a}_{n}=\frac{1}{2}({5}^{{2}^{n-1}}-1)$,
∴bn=$\frac{1}{a_n}$+$\frac{1}{{{a_n}+1}}$=$\frac{2}{{5}^{{2}^{n-1}}-1}+\frac{2}{{5}^{{2}^{n-1}}+1}$=$\frac{4•{5}^{{2}^{n-1}}}{{5}^{{2}^{n}}-1}$,
而$\frac{2}{{a}_{n}}-\frac{2}{{a}_{n+1}}=\frac{4}{{5}^{{2}^{n-1}}-1}-\frac{4}{{5}^{{2}^{n}}-1}$=$\frac{4•{5}^{{2}^{n}}-4-4•{5}^{{2}^{n-1}}+4}{({5}^{{2}^{n-1}}-1)({5}^{{2}^{n}}-1)}$=$\frac{4•{5}^{{2}^{n-1}}}{{5}^{{2}^{n}}-1}$,
∴bn=$\frac{2}{{a}_{n}}$-$\frac{2}{{a}_{n+1}}$;
(3)解:Tn=b1+b2+b3…+bn=$(\frac{2}{{a}_{1}}-\frac{2}{{a}_{2}})+(\frac{2}{{a}_{2}}-\frac{2}{{a}_{3}})+…+(\frac{2}{{a}_{n}}-\frac{2}{{a}_{n+1}})$
=$\frac{2}{{a}_{1}}-\frac{2}{{a}_{n+1}}=1-\frac{2}{\frac{1}{2}({5}^{{2}^{n}}-1)}$=$1-\frac{4}{{5}^{{2}^{n}}-1}$.
点评 本题考查数列的函数特性,考查了等比关系的确定,训练了裂项相消法求数列的和,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
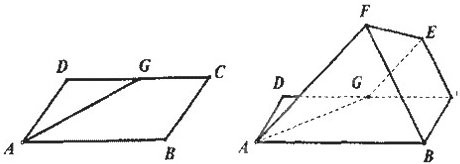
 如图,在直角梯形ABCP中,AB=BC=3,AP=7,CD⊥AP于D,现将△PCD沿线段CD折成60°的二面角P-CD-A,设E,F,G分别是PD,PC,BC的中点.
如图,在直角梯形ABCP中,AB=BC=3,AP=7,CD⊥AP于D,现将△PCD沿线段CD折成60°的二面角P-CD-A,设E,F,G分别是PD,PC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
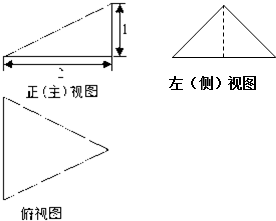
| A. | 2 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com