
分析 (Ⅰ)由已知结合椭圆定义求得动点C的轨迹E的方程;
(Ⅱ)当直线l的斜率不存在时,满足条件的点P的纵坐标为0.当直线l的斜率存在时,设直线l的方程为y=k(x-1).联立直线方程和椭圆方程,利用根与系数的关系求得MN的中点坐标,写出MN的垂直平分线方程,取x=0求得P的纵坐标,结合基本不等式求得点P的纵坐标的取值范围.
解答 解:(Ⅰ)由题意可知,|CA|+|CB|=4,
故动点C的轨迹E是以A,B为焦点的椭圆.
设其方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,则2a=4,a=2,c=1,$b=\sqrt{3}$.
∴椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$(x≠±2);
(Ⅱ)当直线l的斜率不存在时,满足条件的点P的纵坐标为0.
当直线l的斜率存在时,设直线l的方程为y=k(x-1).
联立$\left\{\begin{array}{l}y=k(x-1)\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$得,(3+4k2)x2-8k2x+4k2-12=0.
△=144(1+k2)>0.
设M(x1,y1),N(x2,y2),则${x_1}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}}$.
设MN的中点为Q,则${x_Q}=\frac{{4{k^2}}}{{3+4{k^2}}}$,${y_Q}=k({x_Q}-1)=\frac{-3k}{{3+4{k^2}}}$,
∴$Q(\frac{{4{k^2}}}{{3+4{k^2}}},-\frac{3k}{{3+4{k^2}}})$.
由题意可知k≠0,
又直线MN的垂直平分线的方程为$y+\frac{3k}{{3+4{k^2}}}=-\frac{1}{k}(x-\frac{{4{k^2}}}{{3+4{k^2}}})$.
令x=0,解得${y_P}=\frac{k}{{3+4{k^2}}}=\frac{1}{{4k+\frac{3}{k}}}$.
当k>0时,$4k+\frac{3}{k}≥4\sqrt{3}$,∴$0<{y_P}≤\frac{{\sqrt{3}}}{12}$;
当k<0时,$4k+\frac{3}{k}≤-4\sqrt{3}$,∴$-\frac{{\sqrt{3}}}{12}≤{y_P}<0$.
综上所述,点P纵坐标的取值范围是$[-\frac{{\sqrt{3}}}{12},\frac{{\sqrt{3}}}{12}]$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,体现了分类讨论的数学思想方法,是中档题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 10 | C. | 15 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
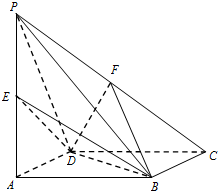 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,∠BAD=60°,侧棱PA⊥底面ABCD,E、F分别是PA、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
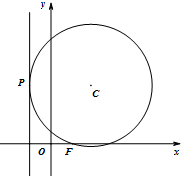 如图,动圆C过点F(1,0),且与直线x=-1相切于点P.
如图,动圆C过点F(1,0),且与直线x=-1相切于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com