
分析 (1)根据G函数的定义,验证函数g(x)是否满足条件.即可
(2)若函数h(x)是G函数根据条件结合函数的单调性进行判断求解即可.
解答 解:(1)是,理由如下:
当x∈[0,1]时,总有g(x)=x2≥0,满足①,
当x1≥0,x2≥0,x1+x2≤1时,
g(x1+x2)=(x1+x2)2=x12+x22+2x1x2≥x12+x22=g(x1)+g(x2),满足②…(4分)
(2)h(x)=2x-b为增函数,h(x)≥h(0)=1-b≥0,
∴b≤1,
由h(x1+x2)≥h(x1)+h(x2),${2}^{{x}_{1}+{x}_{2}}-b≥$${2}^{{x}_{1}}$-b+${2}^{{x}_{2}}$-b,
即b≥1-(${2}^{{x}_{1}}$-1)(${2}^{{x}_{2}}$-1),
∵x1≥0,x2≥0,x1+x2≤1,
∴0≤${2}^{{x}_{1}}$-1≤1,0≤${2}^{{x}_{2}}$-1≤1,x1,x2不同时等于1
∴0≤(${2}^{{x}_{1}}$-1)(${2}^{{x}_{2}}$-1)<1;
∴0<1-(${2}^{{x}_{1}}$-1)(${2}^{{x}_{2}}$-1)≤1,
当x1=x2=0时,1-(${2}^{{x}_{1}}$-1)(${2}^{{x}_{2}}$-1)的最大值为1;
∴b≥1,则b=1,
综合上述:b∈{1} …(12分)
点评 本题主要考查抽象函数的应用,根据抽象函数图象判断条件是否成立是解决本题的关键.考查学生的运算和推理能力.


科目:高中数学 来源: 题型:选择题
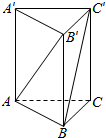 如图,在正三棱柱ABC-A′B′C′中,若AA′=2AB,则异面直线AB′与BC′所成角的余弦值为( )
如图,在正三棱柱ABC-A′B′C′中,若AA′=2AB,则异面直线AB′与BC′所成角的余弦值为( )| A. | 0 | B. | $\frac{3}{8}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 本市明天将有70%的地区降雨 | B. | 本市明天将有70%的时间降雨 | ||
| C. | 明天出行带雨具的可能性很大 | D. | 明天出行不带雨具肯定要淋雨 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 定义域内的减函数 | D. | 定义域内的增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com