
| A. | (1,2) | B. | (-1,2) | C. | (1,+∞) | D. | (2,+∞) |
分析 令x2-x=t,得出关于x的方程x2-x=t的解得分布情况,作出f(t)的函数图象,讨论关于t的方程f(t)=a的解得情况,从而得出方程f(x2-x)=a的解的个数.
解答 解:f(x)的定义域为{x|x≠0},
令x2-x=t(x≠0),则t≥-$\frac{1}{4}$,
且t=-$\frac{1}{4}$或t=0时,方程x2-x=t只有一解,
当-$\frac{1}{4}$<t<0或t>0时,方程x2-x=t有两解,
∴f(t)=$\left\{\begin{array}{l}{t+\frac{1}{t},t>0}\\{lo{g}_{\frac{1}{2}}(-t),-\frac{1}{4}≤t<0}\end{array}\right.$,
∴f(t)在[-$\frac{1}{4}$,0)上单调递增,在(0,1)上单调递减,在(1,+∞)上单调递增,
作出y=f(t)的函数图象如图所示:
由图象可知,当a<2时,关于t的方程f(t)=a无解,
∴方程f(x2-x)=a无解,不符合题意;
当a=2时,关于t的方程f(t)=a有两解t1=-$\frac{1}{4}$,t2=1,
∵x2-x=-$\frac{1}{4}$只有一解,x2-x=1有两解,
∴方程f(x2-x)=a有三解,不符合题意;
当a>2时,关于t的方程f(t)=a有三解,不妨从t1<t2<t3,
显然-$\frac{1}{4}$<t1<0,0<t2<1,t3>1,
又关于x的方程x2-x=ti(i=1,2,3)都有两解,
∴方程f(x2-x)=a有六解,符合题意.
故选D.
点评 本题考查了方程的根与函数图象的关系,属于中档题.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 考前预估难度Pi | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
| 题号 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | × | √ | √ | √ | √ |
| 2 | √ | √ | √ | √ | × |
| 3 | √ | √ | √ | √ | × |
| 4 | √ | √ | √ | × | × |
| 5 | √ | √ | √ | √ | √ |
| 6 | √ | × | × | √ | × |
| 7 | × | √ | √ | √ | × |
| 8 | √ | × | × | × | × |
| 9 | √ | √ | √ | × | × |
| 10 | √ | √ | √ | √ | × |
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 实测答对人数 | |||||
| 实测难度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}$或-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
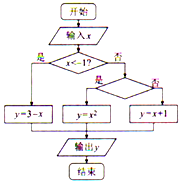 已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )
已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )| A. | x≥1? | B. | x≥-1? | C. | -1≤x≤2? | D. | x≤1? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{19}$ | B. | $\sqrt{13}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com