
【题目】已知函数![]() 是奇函数,且
是奇函数,且![]() 时,有
时,有![]() ,
,![]() ,则不等式
,则不等式![]() 的解集为____.
的解集为____.
【答案】![]()
【解析】
根据条件构造函数g(x)=f(x)﹣x,判断函数g(x)的奇偶性和单调性,结合函数奇偶性和单调性的性质进行转化求解即可.
由x﹣3≤f(x)≤x等价为﹣3≤f(x)﹣x≤0
设g(x)=f(x)﹣x,
又由函数f(x)是定义在R上的奇函数,则有f(﹣x)=﹣f(x),
则有g(﹣x)=f(﹣x)﹣(﹣x)=﹣f(x)+x=﹣[f(x)﹣x]=﹣g(x),
即函数g(x)为R上的奇函数,
则有g(0)=0;
又由对任意0≤x1<x2时,有![]() 1,
1,
则![]() 1,
1,
∵![]() 1,
1,
∴![]() 1<0,
1<0,
即g(x)在[0,+∞)上为减函数,
∵g(x)是奇函数,
∴g(x)在(﹣∞,+∞)上为减函数,
∵f(﹣2)=1,∴g(﹣2)=f(﹣2)﹣(﹣2)=1+2=3;
g(2)=﹣3,g(0)=f(0)﹣0=0,
则﹣3≤f(x)﹣x≤0等价为g(2)≤g(x)≤g(0),
∵g(x)是减函数,
∴0≤x≤2,
即不等式x﹣3≤f(x)≤x的解集为[0,2];
故答案为:[0,2].


科目:高中数学 来源: 题型:
【题目】某校举行运动会,其中三级跳远的成绩在![]() 米以上的进入决赛,把所得的成绩进行整理后,分成
米以上的进入决赛,把所得的成绩进行整理后,分成![]() 组画出频率分布直方图的一部分(如图),已知第
组画出频率分布直方图的一部分(如图),已知第![]() 组的频数是
组的频数是![]() .
.
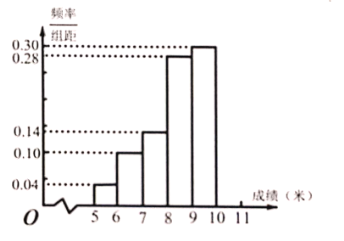
(1)求进入决赛的人数;
(2)用样本的频率代替概率,记![]() 表示两人中进入决赛的人数,求
表示两人中进入决赛的人数,求![]() 得分布列及数学期望.
得分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】依照某发展中国家2018年的官方资料,将该国所有家庭按年收入从低到高的顺序平均分为五组,依次为第一组至第五组,各组家庭的年收入总和占该国全部家庭的年收入总和的百分比如图所示.
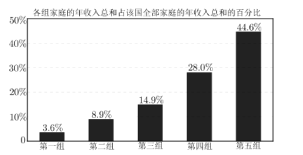
以下关于该国2018年家庭收入的判断,一定正确的是( )
A. 至少有![]() 的家庭的年收入都低于全部家庭的平均年收入
的家庭的年收入都低于全部家庭的平均年收入
B. 收入最低的那![]() 的家庭平均年收入为全部家庭平均年收入的
的家庭平均年收入为全部家庭平均年收入的![]()
C. 收入最高的那![]() 的家庭年收入总和超过全部家庭年收入总和的
的家庭年收入总和超过全部家庭年收入总和的![]()
D. 收入最低的那![]() 的家庭年收入总和超过全部家庭年收入总和的
的家庭年收入总和超过全部家庭年收入总和的![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,
,![]() ,直线
,直线![]() 、
、![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() 。
。
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,是否存在定点
两点,是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 斜率之积为定值,若存在,求出
斜率之积为定值,若存在,求出![]() 坐标;若不存在,请说明理由。
坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若![]() 的值域为
的值域为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)巳![]() ,是否存在这祥的实数
,是否存在这祥的实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 内有且只有一个零点.若存在,求出
内有且只有一个零点.若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .过焦点且垂直于
.过焦点且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 相交所得的弦长为3,直线
相交所得的弦长为3,直线![]() 与椭圆
与椭圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,使得
两点,使得![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,请说明理由!
的取值范围;若不存在,请说明理由!
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.
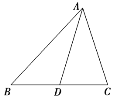
(1)求A;
(2)若AD为BC边上的中线,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() ,在以坐标原点为极点,
,在以坐标原点为极点,![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com